
(2014•张家口二模)已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:
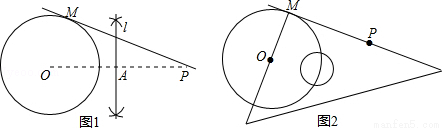
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
C
【解析】
试题分析:(1)连接OM,OA,连接OP,作OP的垂直平分线l可得OA=MA=OP,进而得到∠O=∠AMO,∠AMP=∠MPA,所以∠OMA+∠AMP=∠O+∠MPA=90°,得出MP是⊙O的切线,
(2)直角三角板的一条直角边始终经过点P,它的另一条直角边过圆心O,直角顶点落在⊙O上,所以∠OMP=90°,得到MP是⊙O的切线.
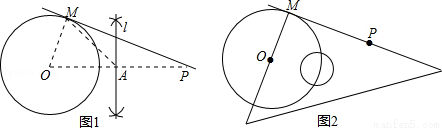
证明:如图1连接OM,OA,
∵连接OP,作OP的垂直平分线l,交OP于点A;
∴OA=OP,
∵以点A为圆心、OA为半径画弧、交⊙O于点M;
∴OA=MA=OP,
∴∠O=∠AMO,∠AMP=∠MPA,
∴∠OMA+∠AMP=∠O+∠MPA=90°
∴OM⊥MP,
∴MP是⊙O的切线,
(2)如图2
∵直角三角板的一条直角边始终经过点P,它的另一条直角边过圆心O,直角顶点落在⊙O上,
∴∠OMP=90°,
∴MP是⊙O的切线.
故两位同学的作法都正确,
故选:C.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源:2014-2015学年广东省广州市番禺区九年级上学期期末模拟质量抽测数学试卷(解析版) 题型:选择题
下列事件中是必然事件的是( ).
(A)抛出一枚硬币,落地后正面向上
(B)明天太阳从西边升起
(C)实心铁球投入水中会沉入水底
(D) 篮球队员在罚球线投篮2次,至少投中一次
篮球队员在罚球线投篮2次,至少投中一次
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 14.2勾股定理的应用练习卷(解析版) 题型:?????
(2013•安顺)如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )

A.8米 B.10米 C.12米 D.14米
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
用反证法证明“若a⊥c,b⊥c,则a∥b”,第一步应假设( )
A.a∥b B.a与b垂直 C.a与b不一定平行 D.a与b相交
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
(2012•温州)下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=﹣2 B.a=﹣1 C.a=1 D.a=2
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.4尺规作图练习卷(解析版) 题型:?????
(2014•福田区模拟)用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
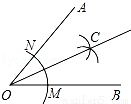
A.(AAS) B.(SAS) C.(ASA) D.(SSS)
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.4尺规作图练习卷(解析版) 题型:?????
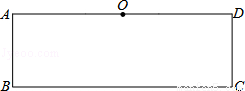
(2014•台湾)如图,矩形ABCD中,AD=3AB,O为AD中点, 是半圆.甲、乙两人想在
是半圆.甲、乙两人想在 上取一点P,使得△PBC的面积等于矩形ABCD的面积其作法如下:
上取一点P,使得△PBC的面积等于矩形ABCD的面积其作法如下:
(甲)延长BO交 于P点,则P即为所求;
于P点,则P即为所求;
(乙)以A为圆心,AB长为半径画弧,交 于P点,则P即为所求.
于P点,则P即为所求.
对于甲、乙两人的作法,下列判断何者正确?( )
A.两人皆正确 B.两人皆错误 C.甲正确,乙错误 D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.1命题、定理与证明练习卷(解析版) 题型:?????
(2014•黄石)以下命题是真命题的是( )
A.等腰梯形是轴对称图形
B.对角线相等的四边形是矩形
C.四边相等的四边形是正方形
D.有两条相互垂直的对称轴的四边形是菱形
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 12.3乘法公式练习卷(解析版) 题型:?????
(2014•台湾)算式999032+888052+777072之值的十位数字为何?( )
A.1 B.2 C.6 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com