已知正方形的面积是25x2+20xy+ny2(x>0,y>0),则正方形的边长是________(用含x、y的代数式表示)
5x+2y
分析:设正方形的边长为a.则a
2=25x
2+20xy+ny
2;然后根据完全平方和公式(a+b)
2=a
2+2ab+b
2来求n值,再来开平方求得a值.
解答:设正方形的边长为a.则
a
2=25x
2+20xy+ny
2∴25x
2+20xy+ny
2是a的完全平方形式,
∴25x
2+20xy+ny
2=(5x)
2+2×5×

xy+
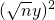
,
∴2×5×

=20,即n=4,
∴正方形的面积是:a
2=25x
2+20xy+4y
2=(5x+2y)
2,
∴a=5x+2y;
故答案为:5x+2y.
点评:本题是完全平方公式的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.

 xy+
xy+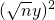 ,
, =20,即n=4,
=20,即n=4,
