
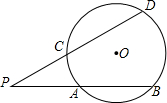
 圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.科目:初中数学 来源: 题型:
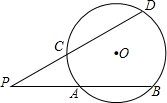 圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.
圆心角度数的一半.类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
 |
| LN |
 |
| LN |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
| 1 |
| 2 |
 |
| RT |
| 1 |
| 2 |
 |
| PQ |
 |
| RT |
 |
| PQ |
 |
| RT |
查看答案和解析>>
科目:初中数学 来源: 题型:
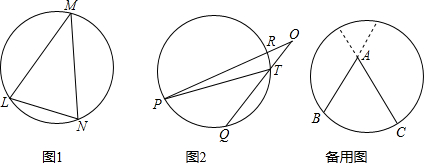
情境一
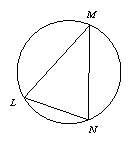
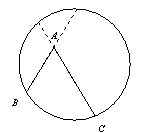
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角.我们还知道:①圆心角的度数等于与它所对的弧的度数,②同弧所对的圆周角相等,都等于该弧所对的圆心角的一半.由此,小明得到一个正确的结论:圆周角的度数等于它所对的弧的度数的一半.如图1,∠LMN=![]()
![]() .
.
问题1 填空:如图1,如果![]() 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
 图
图
1
情境二
小明把顶点在圆外,并且两边都和圆相交的角叫圆外角,并继续探索.
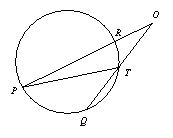
如图2,∵∠PTQ是△OPT的一个外角,
∴∠PTQ=∠O+∠P.
∴∠O=∠PTQ -∠P.
∵圆周角的度数等于它所对的弧的度数的一半(已在情境一中
证明),
∴∠PTQ=![]()
![]() ,∠P=
,∠P=![]()
![]() .
.
∴∠O=∠PTQ -∠P=![]()
![]() -
-![]()
![]() =
=![]() (
(![]() -
-![]() ).
).
经历了上述探索、证明过程,小明发现了“圆外角的度数等于它所夹的较大弧的度数减去较小弧的度数所得差的一半”这个正确结论.
问题2 填空:如图2,如果![]() =80°,
=80°,![]() =20°,那么∠O=______°.
=20°,那么∠O=______°.
问题3 类比情境二的内容,请你就角的顶点在圆内的情况进行探索.写出你的发现,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市联合体中考数学二模试卷(解析版) 题型:解答题

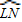 .
.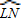 的度数是80,那么∠LMN的度数是______.
的度数是80,那么∠LMN的度数是______.
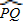 ,∠P=
,∠P=
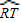 .
.
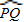 -
-
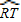 =
= (
(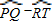 ).
).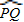 =80°,
=80°, =20°,那么∠O=______°.
=20°,那么∠O=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com