
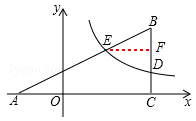
 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).
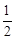 ,求k的值和点B的坐标.
,求k的值和点B的坐标. ,
,
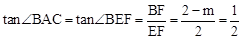 ,解得m=1。
,解得m=1。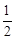 ,由此即可得出结论。
,由此即可得出结论。

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源:不详 题型:填空题
 ,反比例函数
,反比例函数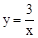 (x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 .
(x>0)的图象分别与AB,BC交于点D,E.连结DE,当△BDE∽△BCA时,点E的坐标为 .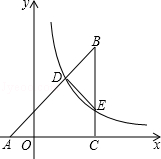
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
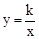 (k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
 ,求反比例函数的解析式;
,求反比例函数的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
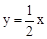 与双曲线
与双曲线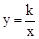 (k>0,x>0)交于点A,将直线
(k>0,x>0)交于点A,将直线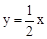 向上平移4个单位长度后,与y轴交于点C,与双曲线
向上平移4个单位长度后,与y轴交于点C,与双曲线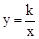 (k>0,x>0)交于点B,若OA=3BC,则k的值为
(k>0,x>0)交于点B,若OA=3BC,则k的值为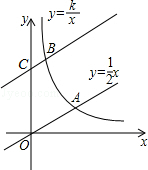
| A.3 | B.6 | C.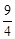 | D.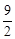 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
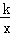 的图象在每一条曲线上,y都随x的增大而增大,
的图象在每一条曲线上,y都随x的增大而增大,查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上,当x1>x2>0时,下列结论正确的是【 】
的图象上,当x1>x2>0时,下列结论正确的是【 】| A.0<y1<y2 | B.0<y2<y1 | C.y1<y2<0 | D.y2<y1<0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,下列说法正确的是
,下列说法正确的是| A.图象经过点(1,﹣3) | B.图象在第二、四象限 |
| C.x>0时,y随x的增大而增大 | D.x<0时,y随x增大而减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com