
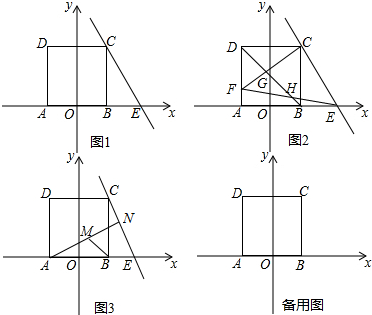
���� ��1����y=kx-2k+4���ɵ�y-4=k��x-2������y=kx-2k+4�����㣬��x��y��ֵ��k�أ��ɵ�$\left\{\begin{array}{l}{x-2=0}\\{y-4=0}\end{array}\right.$�����$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$�������ó�C������꣬���ɵó�������ABCD�ı߳�Ϊ4��
��2����k=-$\frac{4}{3}$ʱ���ó�ֱ��l�Ľ���ʽΪy=-$\frac{4}{3}$x+$\frac{20}{3}$���Ӷ��ó���E�����꣬��FC��CE����DCB=90�㣬��DCF=��BCE���ɵá�DCF�ա�BCE��ASA������DF=BE=5-2=3��AF=1���ó���F��-2��1������ֱ��EF�Ľ���ʽΪy=-$\frac{1}{7}$x+$\frac{5}{7}$��ֱ��BD�Ľ���ʽΪy=-x+2�������õó�G��0��2�������������ľ���ɵó�GH��ֵ��
��3����x���Ͻ�ȡBP=AB������NP��CP����CN=$\frac{1}{2}$AB=2��CP=4$\sqrt{2}$���ɵ�NP��CP-CN=4$\sqrt{2}$-2�����Ե�C��N��P���㹲��ʱ��ȡ�����ֵ������MΪAN���е㣬BΪAP���е㣬�ó��߶�BM�ij��ȵ���СֵΪBM=$\frac{1}{2}$NP��2$\sqrt{2}$-1�������������������Ʊȿɵó�N�����꣮
��� �⣺��1����y=kx-2k+4����y-4=k��x-2����
��ֱ��l��y=kx-2k+4�����㣬��x��y��ֵ��k�أ�
��$\left\{\begin{array}{l}{x-2=0}\\{y-4=0}\end{array}\right.$�����$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$��
��C��2��4����
��������ABCD�ı߳�Ϊ4��
��2����k=-$\frac{4}{3}$ʱ��ֱ��l�Ľ���ʽΪy=-$\frac{4}{3}$x+$\frac{20}{3}$��
��y=0ʱ��x=5��
��E��5��0����
��FC��CE����DCB=90�㣬
���DCF=��BCE��
�ڡ�DCF�͡�BCE�У�
$\left\{\begin{array}{l}{��DCF=��BCE}\\{CD=CB}\\{��CDF=��CBE}\end{array}\right.$��
���DCF�ա�BCE��ASA����
��DF=BE=5-2=3��AF=1��
��F��-2��1��
��ֱ��EF�Ľ���ʽΪy=-$\frac{1}{7}$x+$\frac{5}{7}$��
��B��2��0����D��-2��4����
��ֱ��BD�Ľ���ʽΪy=-x+2��
������$\left\{\begin{array}{l}{y=-\frac{1}{7}x+\frac{5}{7}}\\{y=-x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{1}{2}}\end{array}\right.$��
��G��0��2����
��GH=$\sqrt{��\frac{3}{2}-0��^{2}+��\frac{1}{2}-2��^{2}}$=$\frac{3\sqrt{2}}{2}$��
��3����ͼ3����x���Ͻ�ȡBP=AB������NP��CP��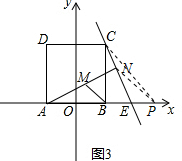
��CN=$\frac{1}{2}$AB=2��CP=4$\sqrt{2}$��
��NP��CP-CN=4$\sqrt{2}$-2��
��C��N��P���㹲��ʱ��ȡ�����ֵ��
�֡�MΪAN���е㣬BΪAP���е㣬
���߶�BM�ij��ȵ���СֵΪBM=$\frac{1}{2}$NP��2$\sqrt{2}$-1��
�����߶�BM�ij��ȵ���СֵΪ2$\sqrt{2}$-1��
��ͼ4��C��N��P���㹲�ߣ�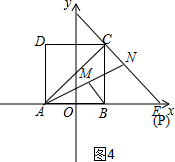
BE=4��EN=4$\sqrt{2}$-2��
��N��x��y����$\frac{y}{BC}$=$\frac{EN}{EC}$����$\frac{y}{4}$=$\frac{4\sqrt{2}-2}{4\sqrt{2}}$�����y=4-$\sqrt{2}$��
$\frac{6-x}{4}$=$\frac{4\sqrt{2}-2}{4\sqrt{2}}$�����x=2+$\sqrt{2}$
���ʱN��2+$\sqrt{2}$��4-$\sqrt{2}$����
���� ������Ҫ������һ�κ������ۺ��⣬�漰һ�κ�������ʽ��ȫ�������ε��ж��������ε����߹�ϵ�����������εĶ�Ӧ�ߵıȣ�����Ĺؼ��ǵ�C��N��P���㹲��ʱ��ȡ��BM�ij��ȵ���Сֵ��


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
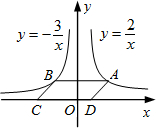 ��ͼ����A�Ƿ���������y=$\frac{2}{x}$��x��0����ͼ��������һ�㣬AB��x�Ტ����������y=-$\frac{3}{x}$��ͼ���ڵ�B����ABΪ����?ABCD�����е�C��D��x���ϣ���?ABCD�����Ϊ��������
��ͼ����A�Ƿ���������y=$\frac{2}{x}$��x��0����ͼ��������һ�㣬AB��x�Ტ����������y=-$\frac{3}{x}$��ͼ���ڵ�B����ABΪ����?ABCD�����е�C��D��x���ϣ���?ABCD�����Ϊ��������| A�� | 3 | B�� | 5 | C�� | 7 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
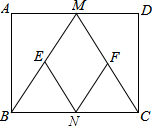 ��ͼ���ھ���ABCD�У�M��N�ֱ��DZ�AD��BC���е㣬E��F�ֱ��DZ�BM��CM���е㣬��AB��AD=1��2ʱ���ı���MENF�������Σ�
��ͼ���ھ���ABCD�У�M��N�ֱ��DZ�AD��BC���е㣬E��F�ֱ��DZ�BM��CM���е㣬��AB��AD=1��2ʱ���ı���MENF�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-x+y����x-y�� | B�� | ��y-1����-1-y�� | C�� | ��x-2����x+1�� | D�� | ��2x+y����2y-x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
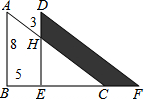 ��ͼ��ԭ�����ص�������ֱ�������Σ�������һ������������BC����ƽ���߶�BE�ľ��룬�͵õ���ͼ�Σ����н�����ȷ���У�������
��ͼ��ԭ�����ص�������ֱ�������Σ�������һ������������BC����ƽ���߶�BE�ľ��룬�͵õ���ͼ�Σ����н�����ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
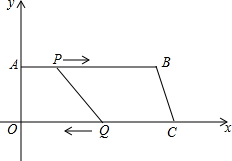 ��ͼ����ƽ��ֱ������ϵ�У��ı���OABC��O��Ϊ����ԭ�㣬A��C����ֱ���y���x���ϣ�AB��OC��OA=8��AB=24��OC=26������P��A��ʼ��AB�����D��1����λ/s���ٶ��˶�������Q��C��ʼ��CO�����O��3����λ/s���ٶ��˶���P��Q�ֱ��A��Cͬʱ��������һ�㵽��ʱ��һ��Ҳֹͣ�����˶�ʱ��Ϊt��
��ͼ����ƽ��ֱ������ϵ�У��ı���OABC��O��Ϊ����ԭ�㣬A��C����ֱ���y���x���ϣ�AB��OC��OA=8��AB=24��OC=26������P��A��ʼ��AB�����D��1����λ/s���ٶ��˶�������Q��C��ʼ��CO�����O��3����λ/s���ٶ��˶���P��Q�ֱ��A��Cͬʱ��������һ�㵽��ʱ��һ��Ҳֹͣ�����˶�ʱ��Ϊt���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
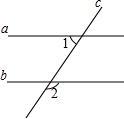 ��ͼ��ʾ����֪a��b����1=50�㣬���2���ڣ�������
��ͼ��ʾ����֪a��b����1=50�㣬���2���ڣ�������| A�� | 50�� | B�� | 70�� | C�� | 110�� | D�� | 130�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com