
【题目】如图,直线y=-x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且 ![]() .
.


(1)求点A的坐标及直线BC的函数关系式;
(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解;对于直线y=x+4,令x=0的y=4,令y=0得x=4,
∴A(4,0),B(0,4),
∴OB=OA=4,
∵OC= ![]() OB,
OB,
∴OC=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,则有 ![]() ,
,
解得 ![]() ,
,
∴直线BC的解析式为y= ![]() x+4.
x+4.
(2)解:如图1中,

当点M在点A的左边时,
∵OB=OA=4,∠AOB=90°,
∴∠ABO=45°,
∴∠CBO+∠MBA=∠MBA+∠MBO=45°,
∴∠CBO=∠OBM,
∵∠CBO+∠BCO=90°,∠BMO+∠OBM=90°,
∴∠BCO=∠BMO,
∴BC=BM,OC=OM=3,
∴M(3,0),
作点M关于直线AB的对称点N,作直线BN交x轴于M ,则∠M BA=∠MBA,点M 满足条件.
∵N(4,1),B(0,4),
∴直线BN的解析式为y= ![]() x+4,令y=0,得x=
x+4,令y=0,得x= ![]() ,
,
∴M ( ![]() ,0),
,0),
综上所述,满足条件的点点M的坐标为(3,0)或( ![]() ,0)
,0)
(3)解:如图2中,
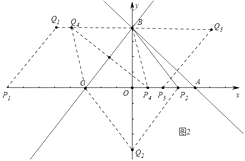
∵BC= ![]() =5,
=5,
当BC为菱形的边时,四边形CPQB,四边形CPQB,四边形BCQP是菱形,此时Q (5,4),Q (5,4),Q (0,4),
当BC是菱形的对角线时,四边形 ![]() 是菱形,可得
是菱形,可得 ![]() (256,4).
(256,4).
综上所述,满足条件的点Q的坐标为(5,4)或(5,4)或(0,4)或( ![]() ,4).
,4).
【解析】(1)分别令y、x等于0,求出直线与x、y轴的交点坐标,由线段OC转化为坐标;(2)分类讨论:点M在点A的左边或在A的右侧,对45度角进行转化,可求出BC关于y轴对称或BM关于y=-x+4的对称直线;(3)可分类讨论,就定线段BC为边,或为对角线,进行分类.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.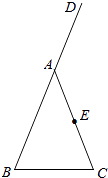
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B两地相距120千米,甲骑自行车以20千米/时的速度由起点A前往终点B,乙骑摩托车以40千米/时的速度由起点B前往终点A.两人同时出发,各自到达终点后停止.设两人之间的距离为s(千米),甲行驶的时间为t(小时),则下图中正确反映s与t之间函数关系的是( )
A.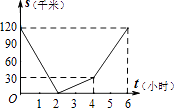
B.
C.
D.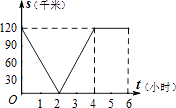
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市从今年1月1日起调整水价,每立方米水费上涨了原价的 ![]() .据了解,某校去年11月份的水费是1800元,而今年1月份的水费是3600元.如果该校今年1月份的用水量比去年11月份的用水量多600m3 .
.据了解,某校去年11月份的水费是1800元,而今年1月份的水费是3600元.如果该校今年1月份的用水量比去年11月份的用水量多600m3 .
(1)该市原来每立方米水价是多少元?
(2)该校开展了“节约每一滴水”的主题活动,采取了有效的节约用水措施,计划今年5月份的用水量较1月份降低20%,那么该校今年5月份应交的水费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.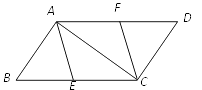
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
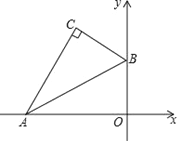
(1)若OB=6cm.①求点C的坐标;②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值= cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com