
 BD,H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.先由正方形的性质得出BD平分∠ABC,∠ABC=90°,由角平分线的性质得到HI=HJ,垂线的定义得到∠HIB=∠HJB=90°,根据一组邻边相等的矩形是正方形证明四边形IBJH是正方形,再利用ASA证明△HMI≌△HNJ,则S四边形MBNH=S正方形HIBJ,根据正方形的面积公式求出S=
BD,H点分别作AB、BC的垂线HI和HJ,垂足分别为I、J.先由正方形的性质得出BD平分∠ABC,∠ABC=90°,由角平分线的性质得到HI=HJ,垂线的定义得到∠HIB=∠HJB=90°,根据一组邻边相等的矩形是正方形证明四边形IBJH是正方形,再利用ASA证明△HMI≌△HNJ,则S四边形MBNH=S正方形HIBJ,根据正方形的面积公式求出S= BH2=
BH2= ;又S四边形MBNH=S△HMB+S△HNB=
;又S四边形MBNH=S△HMB+S△HNB= BH(hM+hN),将数据代入即可求出hM+hN=
BH(hM+hN),将数据代入即可求出hM+hN=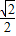 ;
; BD,同(1)可求出S=
BD,同(1)可求出S= BH2=
BH2=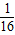 ;hM+hN=
;hM+hN=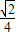 ;
; BH2=
BH2= n2;hM+hN=n.
n2;hM+hN=n.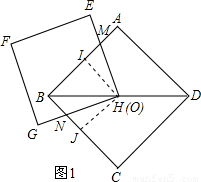 解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,
解:(1)当顶点H和正方形ABCD的中心O重合时,如图1,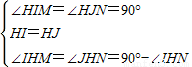 ,
, BH2=
BH2= (
( BD)2=
BD)2= ×(
×(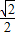 )2=
)2= ;
; BH•hM+
BH•hM+ BH•hN=
BH•hN= BH(hM+hN),
BH(hM+hN), =
= ×
×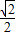 (hM+hN),
(hM+hN),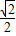 ;
;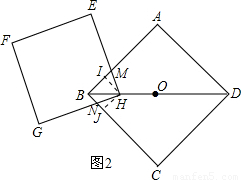 (2)当顶点H为OB的中点时,如图2,
(2)当顶点H为OB的中点时,如图2, BH2=
BH2= (
( BD)2=
BD)2= ×(
×(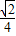 )2=
)2=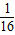 ;
; BH•hM+
BH•hM+ BH•hN=
BH•hN= BH(hM+hN),
BH(hM+hN),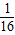 =
= ×
×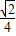 (hM+hN),
(hM+hN),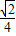 ;
;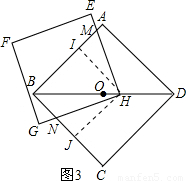 (3)当BH=n时,如图3,
(3)当BH=n时,如图3, BH2=
BH2= n2;
n2; BH•hM+
BH•hM+ BH•hN=
BH•hN= BH(hM+hN),
BH(hM+hN), n2=
n2= n(hM+hN),
n(hM+hN), ,
,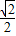 ;(2)
;(2)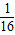 ,
,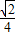 ;(3)
;(3) n2,n.
n2,n.

 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
 21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
21、如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )
(2012•安庆一模)如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图象是( )查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com