
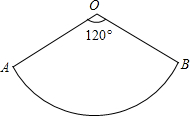
 如图扇形AOB的圆心角为120°,半径为6cm.
如图扇形AOB的圆心角为120°,半径为6cm.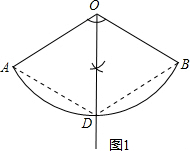 解:(1)如图1所示:作出∠AOB的平分线即可得出;
解:(1)如图1所示:作出∠AOB的平分线即可得出;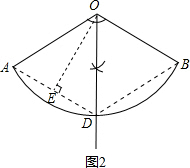
 =3
=3 (cm),
(cm), ×6×3
×6×3 =9
=9 (cm 2),
(cm 2), ×2=18(cm 2).
×2=18(cm 2).

科目:初中数学 来源: 题型:
 小芳同学在出黑板报时画出了一月牙形的图案如图,其中△AOB为等腰直角三角形,以O为圆心,OA为半径作扇形OAB,再以AB的中点C为圆心,以AB为直径作半圆,则月牙形阴影部分的面积S1与△AOB的面积S2之间的大小关系是( )
小芳同学在出黑板报时画出了一月牙形的图案如图,其中△AOB为等腰直角三角形,以O为圆心,OA为半径作扇形OAB,再以AB的中点C为圆心,以AB为直径作半圆,则月牙形阴影部分的面积S1与△AOB的面积S2之间的大小关系是( )| A、S1<S2 | B、S1=S2 | C、S1>S2 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| AB |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 14 |
| 3 |
| 14 |
| 3 |
| 23 |
| 18 |
| 23 |
| 18 |

查看答案和解析>>
科目:初中数学 来源: 题型:
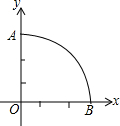 如图,在平面直角坐标系中,以O为圆心、3为半径的圆与两坐标轴围成一个扇形AOB,现将正面分别标有数1、2、3、
如图,在平面直角坐标系中,以O为圆心、3为半径的圆与两坐标轴围成一个扇形AOB,现将正面分别标有数1、2、3、| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
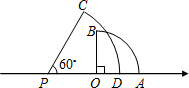 (2013•溧水县二模)如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分(
(2013•溧水县二模)如图,以数轴上的原点O为圆心,6为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,10为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如果两个扇形的圆弧部分( |
| AB |
 |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:013
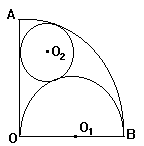
如图: 扇形AOB的半径为R, ∠AOB=90°, 以OB为直径作半圆,圆心为![]() , 若⊙
, 若⊙![]() 与AB
与AB![]() 、⊙
、⊙![]() 和半径OA都相切, 则⊙
和半径OA都相切, 则⊙![]() 的半径长是
的半径长是
[ ]
A.![]() R B.
R B.![]() R
R
C.![]() R D.
R D.![]() R
R
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com