
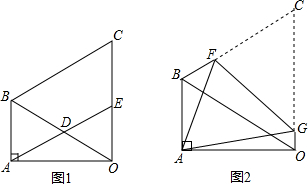
 如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.
如图1,在△OAB中,∠OAB=90°,∠AOB=30°,BA=2.以OB为边,向外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
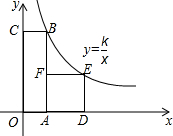 如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=
如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:
在研究气体压强和体积关系的物理实验中,一个气球内充满了一定质量的气体,实验中气体温度保持不变,实验人员记录了实验过程中气球内的气体压强p(kpa)与气体体积V(m3)的数据如下表:| V(m3) | 0.8 | 1.2 | 1.6 | 2.0 | 2.4 |
| p(kpa) | 120 | 80 | 60 | 48 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 乙 | |
| 进价(元/台) | m | m-20 |
| 售价(元/台) | 140 | 110 |
查看答案和解析>>
科目:初中数学 来源: 题型:
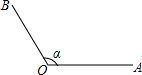 阅读理解:我们知道,角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形,如图一条射线的端点是O,它从起始位置OA按逆时针方向旋转到终止位置OB,形成一个角α,射线OA、OB分别是角α的始边和终边.我们规定,按逆时针方向旋转的角叫做正角,按顺时针方向旋转形成的角叫负角.如果一条射线没有任何旋转,我们称它为零角,这样就可以将角的概念推广到了任意角,由图可知将∠AOB的终边角旋转360°的整数倍后所得的角360°•k+α(k为整数)与∠AOB的终边相同,于是我们可以认为360°•k+α的三角函数值与角α的三角函数值相同.如sin(360°+30°)=sin30°=
阅读理解:我们知道,角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形,如图一条射线的端点是O,它从起始位置OA按逆时针方向旋转到终止位置OB,形成一个角α,射线OA、OB分别是角α的始边和终边.我们规定,按逆时针方向旋转的角叫做正角,按顺时针方向旋转形成的角叫负角.如果一条射线没有任何旋转,我们称它为零角,这样就可以将角的概念推广到了任意角,由图可知将∠AOB的终边角旋转360°的整数倍后所得的角360°•k+α(k为整数)与∠AOB的终边相同,于是我们可以认为360°•k+α的三角函数值与角α的三角函数值相同.如sin(360°+30°)=sin30°=| 1 |
| 2 |
| ||
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com