
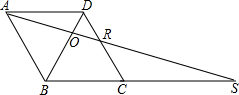
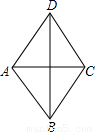
 已知如图:在菱形ABCD中,O是对角线BD上的一点.连结AO并延长,与DC交于点R,与BC的延长线交于点S.若AD=4,∠DCB=60°,BS=10.
已知如图:在菱形ABCD中,O是对角线BD上的一点.连结AO并延长,与DC交于点R,与BC的延长线交于点S.若AD=4,∠DCB=60°,BS=10.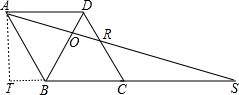 如图,
如图, AB=2,AT=
AB=2,AT= BT=2
BT=2 ,
,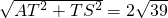 ;
; =
=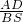 ,即
,即 =
=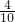 =
= ,
,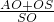 =
=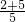 ,
, AS=
AS=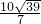
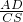 =
=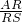 ,即
,即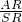 =
= =
= ,
,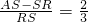 ,
,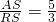 ,
, AS=
AS=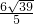 ,
, .
. ,则TS=TB+BS=12,然后根据勾股定理可计算出AS=2
,则TS=TB+BS=12,然后根据勾股定理可计算出AS=2 ;
; =
= ,然后根据性质可得到SO=
,然后根据性质可得到SO=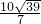 ,利用同样的方法可计算出RS=
,利用同样的方法可计算出RS=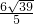 ,然后利用OR=OS-RS进行计算即可.
,然后利用OR=OS-RS进行计算即可.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2008-2009学年江苏省南京市中学九年级(上)月考数学试卷(9月份)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2010年浙江省温州市洞头县中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com