
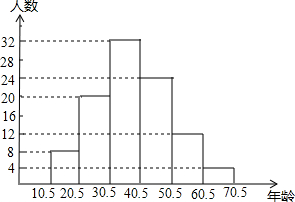
 今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:分析 (1)把直方图给出的所有数据加起来即可求出这次抽样的总人数;
(2)根据抽查的总人数和中位数的定义即可得出答案;
(3)先求出20.5~50.5年龄段的游客所占的百分比,再乘以这天的游客总人数即可得出答案.
解答 解:(1)这次抽样的总人数是:8+20+32+24+12+4=100(人);
故答案为:100;
(2)∵共有100个人,中位数是第50、51个数的平均数,
∴中位数在第三组;
故答案为:三;
(3)20.5~50.5年龄段的游客的比例是:$\frac{20+32+24}{100}$=0.76,
则20.5~50.5年龄段的游客的人数是:600000×0.76=456000(人),
答:20.5~50.5年龄段的游客的人数约为456000人.
点评 此题考查了直方图的应用,用到的知识点是用样本估计总体和中位数,根据直方图给出的数据求出抽查的总人数是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):
某艺术类学校进行绘画特长生的招生工作,每名考生需要参加“素描”“色彩”“速写”三个项目的测试,三个项目的满分均为100分,“素描”“色彩”“速写”按照4:4:2的比例计算得到选手最终成就,现有20名考生报名参加测试,测试结束后,考生的素描成绩如下(单位:分):| 分组 | 人数(频数) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合计 | 20 |
| 项目 成绩 | 素描 | 色彩 | 速写 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.25≤x<1.35 | B. | 1.295≤x<1.305 | C. | 1.25<x<1.35 | D. | 1.295<x<1.305 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
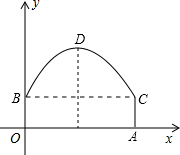 如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系
如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,隧道顶端D到路面的距离为10m,建立如图所示的直角坐标系查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{1}=±1$ | B. | $\sqrt{{{({-3})}^2}}=3$ | C. | $-\sqrt{0.81}=0.9$ | D. | $\sqrt{9}=±3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com