
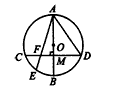
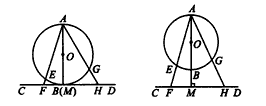
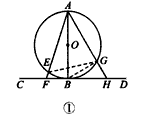
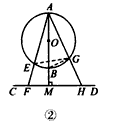
| 解:(1)AE·AF不等于AG2,应该有结论AE·AF=AG·AH, 证明:如图①,连接BG,EG, ∵AB是⊙O的直径,CD是⊙O的切线, ∴∠ABF=∠AGB=90°, ∴∠BAF+∠BFA=90°, ∴∠AGE+∠BGE=90°, ∴∠BAF+∠BFA=∠AGF+∠BGE, 而∠BAF=∠BGE, ∴∠BFA=∠AGE, 又∠FAH=∠GAE, ∴△FAH∽△GAE, ∴ 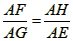 ∴所以AE·AF=AG·AH; |
 |
| (2)(1)中探求的结论还成立, 证明:如图②连接EG,BG, ∵AB是⊙O的直径,AM⊥CD,∠AMF=∠AGB=90°, ∴∠AFM+∠FAM=∠ACE+∠BGE=90°, 而∠FAM=∠BGE, ∴∠AFM=∠AGE, 又∠FAH=∠GAE, ∴△FAH∽△GAE, ∴ 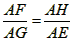 ∴ AE·AF=AG·AH。 |
 |


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)解不等式
(1)解不等式| 2x-1 |
| 3 |
| 5x+1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
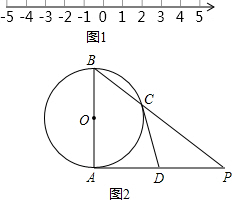
 (2010•资阳)如图甲,已知AB是⊙O的直径,直线l与⊙O相切于点B,直线m垂直AB于点C,交⊙O于P、Q两点.连接AP,过O作OD∥AP交l于点D,连接AD与m交于点M.
(2010•资阳)如图甲,已知AB是⊙O的直径,直线l与⊙O相切于点B,直线m垂直AB于点C,交⊙O于P、Q两点.连接AP,过O作OD∥AP交l于点D,连接AD与m交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com