
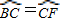
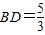 ,AE=4,求∠BCD的正切值.
,AE=4,求∠BCD的正切值.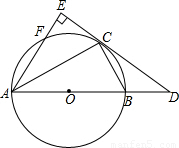
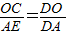 ,设OC=t,代入即可得出t的值,即可求出CO,AB,再由切割线定理得出CD,则可证明△DBC∽△DCA,得出比例式BC:AC,根据∠BCD=∠2
,设OC=t,代入即可得出t的值,即可求出CO,AB,再由切割线定理得出CD,则可证明△DBC∽△DCA,得出比例式BC:AC,根据∠BCD=∠2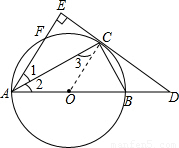 (1)DE是⊙O的切线(1分)
(1)DE是⊙O的切线(1分)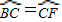 ,∴∠1=∠2(2分)
,∴∠1=∠2(2分)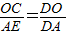
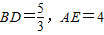
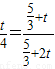
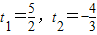
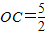 (5分)
(5分)
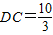 (6分)
(6分)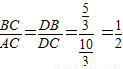 (7分)
(7分)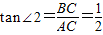
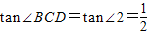 (8分)
(8分)

科目:初中数学 来源: 题型:
 如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为
如图,已知A是半径为1的⊙O上一点,以A为圆心,AO为半径画弧交⊙O于点B、C;以C为圆心,CO为半径画弧交⊙O于点D、A.则图中阴影面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(2012•梁子湖区模拟)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB. | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么,| a+b |
| 2 |
| ab |
| a |
| b |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b+c |
| 3 |
| 3 | abc |
| 3 | abc |
| a+b |
| 2 |
| ab |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com