
 ,而它的两邻边a、b的长满足m2+a2m-12a=0,m2+b2m-12b=0(m≠0),则矩形的周长为________.
,而它的两邻边a、b的长满足m2+a2m-12a=0,m2+b2m-12b=0(m≠0),则矩形的周长为________. ,即可知道a、b的平方和,即可得到一个关于m的方程,从而求解.
,即可知道a、b的平方和,即可得到一个关于m的方程,从而求解.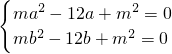 ,
, …①
…①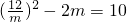 ?m3+5m2-72=0?(m-3)(m2+8m+24)=0?m=3,
?m3+5m2-72=0?(m-3)(m2+8m+24)=0?m=3,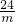 =8.
=8.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com