
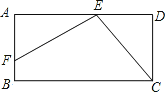
【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
【答案】(1)证明见解析;(2)6cm.
【解析】(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.
(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.
(1)证明:∵EF⊥CE,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,
∴∠AEF=∠ECD.
在Rt△AEF和Rt△DEC中,
∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.
∴△AEF≌△DCE.
(2)解:∵△AEF≌△DCE.
AE=CD.
AD=AE+4.
∵矩形ABCD的周长为32cm,
∴2(AE+AE+4)=32.
解得,AE=6(cm).
答:AE的长为6cm.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 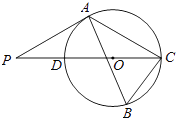
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由“※”组成的图案和算式,解答问题:
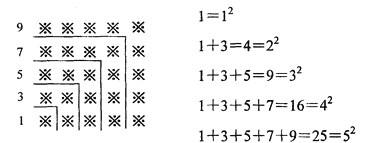
(1)请猜想1+3+5+7+9+…+19=_______________________;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1) =___________;
(3)请用上述规律计算:51+53+55+…+2011+2013.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
求证:∠P=90°﹣![]() ∠C;
∠C;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E. 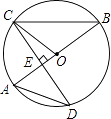
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4 ![]() ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
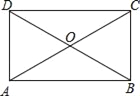
A. ①②③ B. ②③④ C. ②⑤⑥ D. ④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A,B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= . 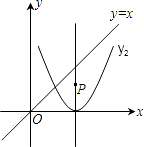
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1 . 设CB1交AB于点D,A1B1分别交AB,AC于点E,F.
(1)求证:△BCD≌△A1CF;
(2)若旋转角ɑ为30°,
①请你判断△BB1D的形状;
②求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com