
 与x轴、y轴相交于点B、C,点A的坐标为(-4,-3).点P是射线AC上一个动点,点P从A点出发沿x轴的正方向以每秒1个单位的速度匀速移动,过点P作平行于BC的直线L与x轴、y轴相交于点M、N,设
与x轴、y轴相交于点B、C,点A的坐标为(-4,-3).点P是射线AC上一个动点,点P从A点出发沿x轴的正方向以每秒1个单位的速度匀速移动,过点P作平行于BC的直线L与x轴、y轴相交于点M、N,设 点P运动的时间为t(秒).
点P运动的时间为t(秒). BC;
BC; BC,此时t=6s或t=10s;
BC,此时t=6s或t=10s; •t•3=
•t•3= t;S△NAP=
t;S△NAP= •t•
•t• (4-t)=-
(4-t)=- t2+
t2+ t;
t;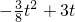 ;
; t-
t- •t•
•t• (t-4)=-
(t-4)=- t2+3t;
t2+3t; •t•
•t• (t-4)=
(t-4)= t2-3t.
t2-3t.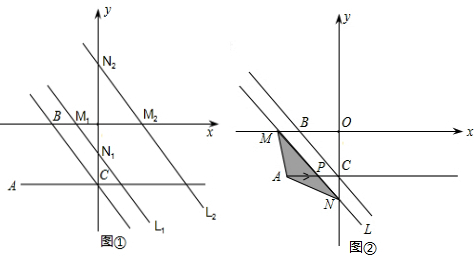
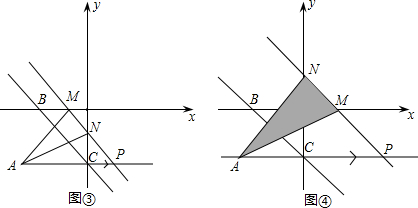
 ,直角三角形CPN中,有AC=4,AP=t,那么可表示出CP,再根据∠CPN的正切值,那么CN的值就能表示出来了.这样三角形APN的面积也就能表示出来了.那么他们的面积和即三角形AMN的面积就能求出来了.也就得出了S与t的函数关系式.
,直角三角形CPN中,有AC=4,AP=t,那么可表示出CP,再根据∠CPN的正切值,那么CN的值就能表示出来了.这样三角形APN的面积也就能表示出来了.那么他们的面积和即三角形AMN的面积就能求出来了.也就得出了S与t的函数关系式.

科目:初中数学 来源: 题型:
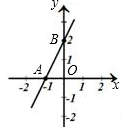 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2x |
| 1 |
| 2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源:2011届宁夏银川市初三上学期期末数学卷 题型:解答题
如图①,直线 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
(1)写出A、B、C三点的坐标,并求抛物线的解析式;(5分)
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;(3分)
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com