
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

【答案】(1)![]() ;(2)存在,△PAC的面积最大值为
;(2)存在,△PAC的面积最大值为![]() ,点P的坐标为(
,点P的坐标为(![]() ,
,![]() );(3)点M的坐标为:
);(3)点M的坐标为: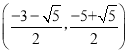 或
或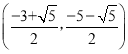 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)由一次函数解析式求得A、C两点的坐标,然后代入到二次函数解析式,用待定系数法求解;
(2)过点P作PQ⊥x轴,垂足为Q,直线PQ,AC交于点P,设点P的坐标为(![]() ,
,![]() ),则点D的坐标为(
),则点D的坐标为(![]() ,
,![]() ),根据两点间距离公式求得PD =
),根据两点间距离公式求得PD =![]() ,然后根据三角形面积公式求得
,然后根据三角形面积公式求得![]() =
=![]() =
=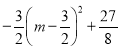 ,由此根据二次函数的性质分析最值;
,由此根据二次函数的性质分析最值;
(3)分情况讨论:当点M在对称轴左侧时,构造矩形EFCG,设点M的坐标为(![]() ,
,![]() ),利用AAS定理证明△MEN≌△CFM,然后结合抛物线对称轴求得MF=
),利用AAS定理证明△MEN≌△CFM,然后结合抛物线对称轴求得MF=![]() =
=![]() ,NE=
,NE=![]() ,从而列方程求解;作MF⊥y轴,垂足为F,MF交对称轴于点E;设点M的坐标为(
,从而列方程求解;作MF⊥y轴,垂足为F,MF交对称轴于点E;设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,然后列方程求解;当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.设点M的坐标为(
,然后列方程求解;当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.设点M的坐标为(![]() ,
,![]() ),然后结合抛物线对称轴求得ME=
),然后结合抛物线对称轴求得ME= ![]() =
=![]() ,CF=
,CF= ![]() =
= ![]() ,然后列方程求解;作ME⊥对称轴,垂足为E,ME交NC,交点为F.设点M的坐标为(
,然后列方程求解;作ME⊥对称轴,垂足为E,ME交NC,交点为F.设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,然后列方程求解.
,然后列方程求解.
解:(1)![]() 交x轴于A(-3,0),交y轴于C(0,-3),
交x轴于A(-3,0),交y轴于C(0,-3),
∵抛物线![]() 经过点A(-3,0),点C(0,-3),
经过点A(-3,0),点C(0,-3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为:![]() ;
;
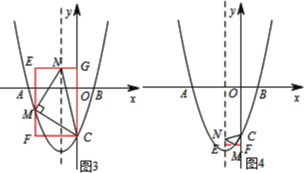
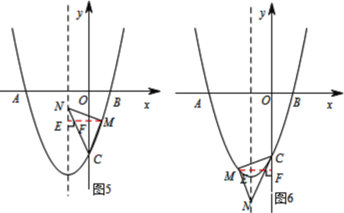
(2)如图2,过点P作PQ⊥x轴,垂足为Q,直线PQ,AC交于点P,
设点P的坐标为(![]() ,
,![]() ),则点D的坐标为(
),则点D的坐标为(![]() ,
,![]() ),
),
∴线段PD的长为:(![]() )-(
)-(![]() )=
)=![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() =
=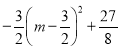 ,
,
∵![]() ,∴当
,∴当![]() 时候,△PAC的面积又最大值,最大值为
时候,△PAC的面积又最大值,最大值为![]() ,
,
此时点P的坐标为(![]() ,
,![]() );
);
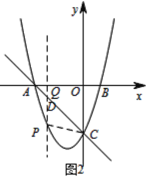
(3)①如图3,当点M在对称轴左侧时,构造矩形EFCG,设点M的坐标为(![]() ,
,![]() ),
),
∵△NMC是以∠NMC为直角的等腰直角三角形
∴∠NME+∠CMF=90°,∠FCM+∠CMF=90°
∴∠NME=∠FCM
又∵∠E=∠F=90°,MN=MC
∴△MEN≌△CFM,
∵抛物线![]() 的对称轴为直线x=-1,
的对称轴为直线x=-1,
∴MF=![]() =
=![]() ,NE=
,NE=![]() ,
,
∵MF=NE,∴![]() ,
,
解得![]() (舍),
(舍),![]() ,
,
故点M的坐标为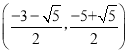 ;
;
②如图6,作MF⊥y轴,垂足为F,MF交对称轴于点E;
设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,
,
由①同理可证△MNE≌△CFM,
∵ME=CF,故![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
故点M的坐标为(![]() ,
,![]() );
);
③如图5,当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.
设点M的坐标为(![]() ,
,![]() ),
),
由①同理可证△MEN≌△MFC,抛物线对称轴为直线x=-1,
则ME= ![]() =
=![]() ,CF=
,CF= ![]() =
= ![]() ,
,
∵ME=CF,∴![]() ,解得:
,解得:![]() (舍),
(舍),![]() ,
,
故的点M的坐标 为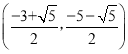 ;
;
④如图4,作ME⊥对称轴,垂足为E,ME交NC,交点为F.
设点M的坐标为(![]() ,
,![]() ),则ME=
),则ME= ![]() ,CF=
,CF= ![]() ,
,
由①同理可证△MNE≌△CFM,
∵ME=CF,故![]() ,
,
解得:![]() ,
,![]() (舍),
(舍),
故点M的坐标为(![]() ,
,![]() );
);
综上可得点M的坐标为: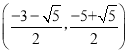 或
或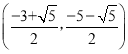 或(
或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
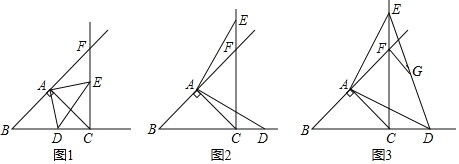
【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(不与点B、点C重合),将线段AD绕A逆时针旋转90°得到线段AE,作射线BA与射线CE,两射线交于点F.
(1)若点D在线段BC上,如图1,请直接写出CD与EF的关系.
(2)若点D在线段BC的延长线上,如图2,(1)中的结论还成立吗?请说明理由.
(3)在(2)的条件下,连接DE,G为DE的中点,连接GF,若tan∠AEC=![]() ,AB=
,AB=![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
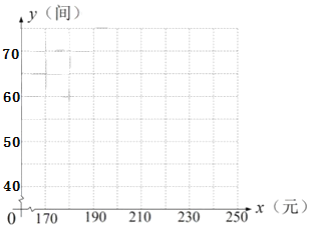
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学疫情期间为了切实抓好“停课不停学”活动,借助某软件平台随机抽取了该校部分学生的在线学习时间,并将结果绘制成如下两幅不完整的统计图.

请你根据以上信息回答下列问题
(1)本次调查的人数为 , 学习时间为7小时的所对的圆心角为 ;
(2)补全频数分布直方图;
(3)若全校共有学生1800人,估计有多少学生在线学习时间不低于8个小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
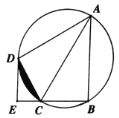
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位老师同住一小区,该小区与学校相距![]() 米.甲从小区步行去学校,出发
米.甲从小区步行去学校,出发![]() 分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为
分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为![]() 米/分,甲步行的速度比乙步行的速度每分钟快
米/分,甲步行的速度比乙步行的速度每分钟快![]() 米.设甲步行的时间为
米.设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 与折线
与折线![]() 分别表示甲、乙离小区的路程
分别表示甲、乙离小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
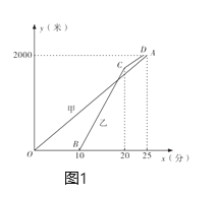
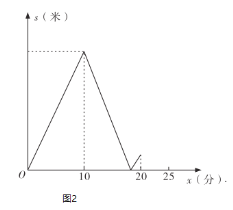
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线![]() 的解析式;
的解析式;
(3)在图2中,画出当![]() 时,
时,![]() 关于
关于![]() 的函数的大致图象.
的函数的大致图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com