
已知二次函数y=x2-x+c.
(1)若点A(-1,n),B(2,2n-1)在二次函数y=x2-x+c的图象上,求此二次函数的最小值;
(2)若点D(x1,y1),E(x2,y2),P(m,m)(m>0)在抛物线y=x2-x+c上,且D,E两点关于坐标原点成中心对称,连接PO,当2![]() ≤PO≤
≤PO≤![]() +2时,试判断直线DE与抛物线y=x2-x+c+
+2时,试判断直线DE与抛物线y=x2-x+c+![]() 的交点个数,并说明理由.
的交点个数,并说明理由.
解:(1)法1:由题意得 ![]()
解得 ![]()
法2:∵抛物线y=x2-x+c的对称轴是x=![]() ,
,
且![]() -(-1) =2-
-(-1) =2-![]() ,∴A,B两点关于对称轴对称.
,∴A,B两点关于对称轴对称.
∴n=2n-1
∴n=1,c=-1.
∴有 y=x2-x-1
=(x-![]() )2-
)2-![]() .
.
∴二次函数y=x2-x-1的最小值是-![]() .
.
(2)∵点P(m,m)(m>0),
∴PO=![]() m.
m.
∴2![]() ≤
≤![]() m≤
m≤![]() +2.
+2.
∴2≤m≤1+![]() .
.
法1:∵点P(m,m)(m>0)在二次函数y=x2-x+c的图象上,
∴m=m2-m+c,即c=-m2+2m.
∵开口向下,且对称轴m=1,
∴当2≤m≤1+![]() 时,
时,
有 -1≤c≤0.(6分)
法2:∵2≤m≤1+![]() ,
,
∴1≤m-1≤![]() .
.
∴1≤(m-1)2≤2.
∵点P(m,m)(m>0)在二次函数y=x2-x+c的图象上,
∴m=m2-m+c,即1-c=(m-1)2.
∴1≤1-c≤2.
∴-1≤c≤0.
∵点D,E关于原点成中心对称,
法1:∴x2=-x1,y2=-y1.
∴![]()
∴2y1=-2x1,y1=-x1.
设直线DE:y=kx.
有 -x1=kx1.
由题意,存在x1≠x2.
∴存在x1,使x1≠0.
∴k=-1.
∴直线DE:y=-x.
法2:设直线DE:y=kx.
则根据题意有 kx=x2-x+c,即x2-(k+1)x+c=0.
∵-1≤c≤0,
∴(k+1)2-4c≥0.
∴方程x2-(k+1)x+c=0有实数根.
∵x1+x2=0,
∴k+1=0.
∴k=-1.
∴直线DE:y=-x.
若 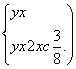 则有 x2+c+
则有 x2+c+![]() =0.
=0.
即 x2=-c-![]() .
.
①当-c-![]() =0时,即c=-
=0时,即c=-![]() 时,方程x2=-c-
时,方程x2=-c-![]() 有相同的实数根,
有相同的实数根,
即直线y=-x与抛物线y=x2-x+c+![]() 有唯一交点;
有唯一交点;
②当-c-![]() >0时,即c<-
>0时,即c<-![]() 时,即-1≤c<-
时,即-1≤c<-![]() 时,
时,
方程x2=-c-![]() 有两个不同实数根,
有两个不同实数根,
即直线y=-x与抛物线y=x2-x+c+![]() 有两个不同的交点;
有两个不同的交点;
③当-c-![]() <0时,即c>-
<0时,即c>-![]() 时,即-
时,即-![]() <c≤0时,
<c≤0时,
方程x2=-c-![]() 没有实数根,
没有实数根,
即直线y=-x与抛物线y=x2-x+c+![]() 没有交点.
没有交点.


科目:初中数学 来源: 题型:
(本题满分10分)已知二次函数y=x2+bx-3的图像经过点P(-2,5).
(1)求b的值,并写出当0<x≤3时y的取值范围;
(2)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图像上.
①试比较y1和y2的大小;
②当m取不小于5的任意实数时,请你探索:y1、y2、y3能否作为一个三角形
三边的长,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年蒙城六中九年级(上)第一次教学质量检测数学卷 题型:解答题
已知二次函数y=x2-2x-3.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)画出此抛物线图象;
(3)利用图象回答下列问题:
①方程x2-2x-3=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
查看答案和解析>>
科目:初中数学 来源:2011届江苏省太仓市九年级上学期期中考试数学卷 题型:选择题
已知二次函数y=x2-4x+3的图象是由y=x2+2x-1的图象先向上平移一个单位,再向
A.左移3个单位 B.右移3个单位 C.左移6个单位 D.右移6个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com