
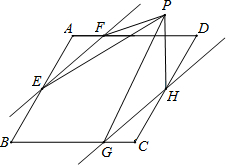
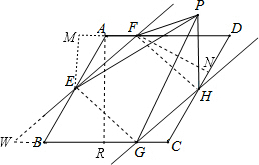
 如图,在边长为4的菱形ABCD中,∠B=60°,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于
如图,在边长为4的菱形ABCD中,∠B=60°,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于


 ,
,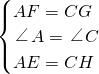 ,
, EF×hEF+
EF×hEF+ GH×hGH=
GH×hGH= S平行四边形EFHG;
S平行四边形EFHG; AE=1,
AE=1, ,
, ×AF×ME=
×AF×ME= ×1×
×1× =
=
 ,
,
 ,
, DF=
DF= ×(4-1)=
×(4-1)= ,
,
 ,
, DH×FN=
DH×FN= ×(4-2)×
×(4-2)×
 =
=
 ,
,
 ,
, -
-
 -
-
 -
-
 -
-
 =4
=4 ,
, S平行四边形EFHG=2
S平行四边形EFHG=2 ,
,

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
如图是一个边长为60cm的立方体ABCD—EFGH,一只甲虫在菱EF上且距F点10cm的P处,它要爬到顶点D,需要爬行的最近距离是( )

A.130B.![]() C.
C.![]() D.不确定
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com