解:(1)∵四边形ABCD是矩形,DE平分∠ADC,
∴∠CDE=∠CED=45°;
∴EC=DC,
又∵∠ADB=30°,
∴∠CDO=60°;
又∵因为矩形的对角线互相平分,
∴OD=OC;
∴△OCD是等边三角形;
∴∠DCO=60°,∠OCB=90°-∠DCO=30°;
∵DE平分∠ADC,∠ECD=90°,
∠CDE=∠CED=45°,
∴CD=CE=CO,
∴∠COE=∠CEO;
∴∠COE=(180°-30°)÷2=75°;
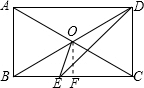
(2)过O作OF⊥BC于F,
∵AO=CO,
∴BF=CF,
∴OF=

AB=2,
∵∠ADB=30°,AB=4,
∴AC=8,
∴BC=

=4

,
∴BF=CF=2

,
∵CD=CE=4,
∴EF=CE-CF=4-2

,
在Rt△OFE中,
OE=
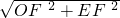
=4

.
分析:(1)四边形ABCD是矩形,DE平分∠ADC”知∠CDE=∠CED=45°,又∠ADB=30°,所以∠CDO=60°,由矩形的特征“对角线互相平分”可知OD=OC,故△OCD是等边三角形,从而有OC=OD=CE,∠DCO=60°,∠OCB=30°,进而求得∠COE=75°;
(2)过O作OF⊥BC于F,利用已知条件求出BC和OF的值,再利用勾股定理即可求出OE的长.
点评:本题考查了矩形的性质、等边三角形的判定和性质以及勾股定理的运用,题目综合性很强.

 矩形ABCD中,AC、BD相交于点O,且∠ADB=30°,∠ADC的平分线交BC于E,连接OE.
矩形ABCD中,AC、BD相交于点O,且∠ADB=30°,∠ADC的平分线交BC于E,连接OE.
 AB=2,
AB=2, =4
=4 ,
, ,
, ,
,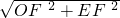 =4
=4 .
.
