Question

设点P是△ABC内任意一点．现给出如下结论：

①过点P至少存在一条直线将△ABC分成周长相等的两部分；

②过点P至少存在一条直线将△ABC分成面积相等的两部分；

③过点P至多存在一条直线将△ABC分成面积相等的两部分；

④△ABC内存在点Q，过点Q有两条直线将其平分成面积相等的四个部分．

其中结论正确的是　  　．（写出所有正确结论的序号）

 

Answer 1

【答案】

①②④

【解析】

试题分析：结论①正确。理由如下：

如答图1所示，设点P为△ABC内部的任意一点，经过点P的直线l将△ABC分割后，两侧图形的周长分别为C₁，C₂（C₁，C₂中不含线段DE），

在直线l绕点P连续的旋转过程中，周长由C₁＜C₂（或C₁＞C₂）的情形，逐渐变为C₁＞C₂（或C₁＜C₂）的情形，在此过程中，一定存在C₁=C₂的时刻，因此经过点P至少存在一条直线平分△ABC的周长。故结论①正确。

结论②正确。理由如下：

如答图1所示，

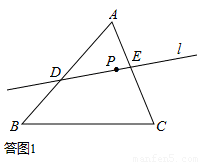
设点P为△ABC内部的任意一点，经过点P的直线l将△ABC分割后，两侧图形的面积分别为S₁，S₂，

在直线l绕点P连续的旋转过程中，面积由S₁＜S₂（或S₁＞S₂）的情形，逐渐变为S₁＞S₂（或S₁＜S₂）的情形，在此过程中，一定存在S₁=S₂的时刻，因此经过点P至少存在一条直线平分△ABC的面积。故结论②正确。

结论③错误。理由如下：

如答图2所示，

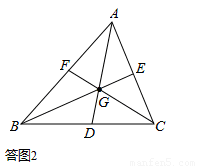
AD、BE、CF为三边的中线，则AD、BE、CF分别平分△ABC的面积，而三条中线交于重心G，则经过重心G至少有三条直线可以平分△ABC的面积。故结论③错误。

结论④正确。理由如下：

如答图3所示，

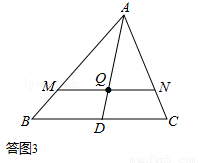
AD为△ABC的中线，点M、N分别在边AB、AC上，MN∥BC，且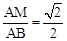，MN与AD交于点Q。

∵MN∥BC，∴△AMN∽△ABC。

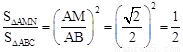∴，即MN平分△ABC的面积。

又∵AD为中线，

∴过点Q的两条直线AD、MN将△ABC的面积四等分。故结论④正确。

综上所述，正确的结论是：①②④。