练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列不在等腰三角形对称轴上的是


    1. A.
      顶角的平分线
    2. B.
      一边的中线
    3. C.
      底边上的中线
    4. D.
      底边上的高线
    B
    分析：此题可依据等腰三角形三线合一的性质和轴对称图形的性质进行判断．
    解答：等腰三角形的对称轴是顶角平分线、底边上的中线、底边上的高线所在直线．
    故选B．
    点评：此题主要考查等腰三角形的对称性和三线合一的性质．需要注意的是轴对称图形的对称轴是条直线，而三角形的角平分线、中线和高线是线段，不要将概念弄混淆了．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、如图，在△ABC中，AB=AC，DE=EC，DH∥BC，EF∥AB，HE的延长线与BC的延长线相交于点M，点G在BC上，且∠1=∠2，不添加辅助线，解答下列问题：
    （1）找出一个等腰三角形；（不包括△ABC）
    （2）找出三对相似三角形；（不包括全等三角形）
    （3）找出两对全等三角形，并选出一对进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    2、下列四个命题：
    ①如果一条直线上的两个不同的点到另一条直线的距离相等，那么这两条直线平行；
    ②反比例函数的图象是轴对称图形，它只有一条对称轴；
    ③等腰三角形一腰上的高等于腰长的一半，则底角的度数为75度；
    ④在同圆或等圆中，相等的圆周角所对的弧相等．
    其中不正确的命题有（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，等腰三角形与正三角形的形状有着差异，我们把它与正三角形的接近程度称为等腰三角形的“正度”，在研究“正度”时，应符合下面四个条件：①“正度”的值是非负数；②“正度”值越小，表示等腰三角形越接近正三角形；③相似的等腰三角形“正度”要相等；④正三角形的“正度”是0．例如：
    设等腰三角形的底和腰分别为a，b，底角和顶角分别为α，β．
    可用|sinα-
    		3
    2
    |    表示等腰三角形的“正度”，|sinα-
    		3
    2
    |    的值越小，α越接近60°，表示等腰三角形越接近正三角形，且当两个等腰三角形相似时，它们的底角相等，显然，它们的“正度”|sinα-
    		3
    2
    |    也相等，当α=60°时，|sinα-
    		3
    2
    |=0    ．
    而如果用
    a
    b
    表示等腰三角形的“正度”，就不符合要求，因为此时正三角形的正度是1！
    解答下列问题：
    甲同学认为：可用|a-b|表示等腰三角形的“正度”，|a-b|的值越小，表示等腰三角形越接近正三角形；
    乙同学认为：可用|α-β|表示等腰三角形的“正度”，|α-β|的值越小，表示等腰三角形越接近正三角形．
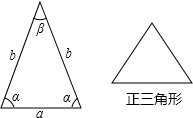    精英家教网（1）他们的说法合理吗？为什么？
    （2）对你认为不合理的方案加以改进，使其合理；
    （3）请你再给出一种衡量等腰三角形“正度”的合理的表达式，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•吉安模拟）如图，有一张矩形纸片ABCD，已知AB=2，BC=4，若点E是AD上的一个动点（与点A不重合），且0＜AE≤2，沿BE将△ABE对折后，点A落到点P处，连接PC．
    （1）下列说法正确的序号是
    ①②④
    ①②④

    ①．△ABE与△PBE关于直线BE对称
    ②．以B为圆心、BA的长为半径画弧交BC于H，则点P在AH上（点A除外）
    ③．线段PC的长有可能小于2．
    ④．四边形ABPE有可能为正方形
    （2）试求下列情况下的线段PC的长（可用计算器，精确到0.1）．
    ①以P、C、D为顶点的三角形是等腰三角形；
    ②直线CP与BE垂直．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

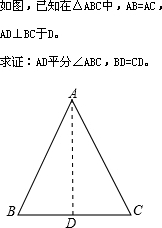    小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时，画出图形，写出“已知”、“求证”（如图）．
    （1）请你帮助小明完成证明过程．
    （2）请你作出判断：小明写出的“已知”、“求证”是否完整？在横线上填“是”或“否”．
    是
    是

    （3）做完（1）后，小明模仿老师上课时的方法，又提出了如下几个问题：
    如：①若将题中“AD⊥BC”与“AD平分∠ABC”的位置交换，得到的是否仍是真命题？
    ②若将题中“AD⊥BC”与“BD=CD”的位置交换，得到的是否仍是真命题？请你作出判断，在下列横线上填写“是”或“否”：①
    是
    是
     ②
    是
    是
     并对②的判断作出证明．（若是则写出证明过程；若不是则举出一个反例）

    查看答案和解析>>

    同步练习册答案