
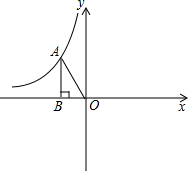 如图,过反比例函数
如图,过反比例函数 图象上的一点A作x轴的垂线段AB,再连接AO,构成直角三角形ABO,S△ABO=3,请你求出该反比例函数的关系式,并说出它的两条性质.
图象上的一点A作x轴的垂线段AB,再连接AO,构成直角三角形ABO,S△ABO=3,请你求出该反比例函数的关系式,并说出它的两条性质. |k|=3,
|k|=3,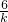 ,
, |k|,及图象位于第二象限求出k的值,得到反比例函数的解析式,再根据反比例函数的性质作答即可.
|k|,及图象位于第二象限求出k的值,得到反比例函数的解析式,再根据反比例函数的性质作答即可. 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为 |k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义,同时考查了反比例函数的图象性质:反比例函数的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义,同时考查了反比例函数的图象性质:反比例函数的图象是双曲线;当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大. 

科目:初中数学 来源: 题型:
 如图,过反比例函数y=
如图,过反比例函数y=| 9 |
| x |
| A、S1>S2 |
| B、S1=S2 |
| C、S1<S2 |
| D、大小关系不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |

查看答案和解析>>
科目:初中数学 来源: 题型:
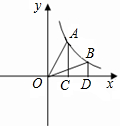
如图10,已知直线![]() (
(![]() )交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM
)交x轴、y轴于A、B两点,点C、M分别在线段OA、AB上,且OC=2CA,AM![]() =2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,显然点E在y轴上, 点F在直线l上;取线段EO中点N,将△ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的反比例函数图象为
=2MB,连接MC,将△ACM绕点M旋转180°,得到△FEM,显然点E在y轴上, 点F在直线l上;取线段EO中点N,将△ACM沿MN所在直线翻折,得到△PMG,其中P与A为对称点.记:过点F的反比例函数图象为![]() ,过点M且以B为顶点的
,过点M且以B为顶点的![]() 二次函数图象为
二次函数图象为![]() ,过点P且以M为顶点的二次函数图象为
,过点P且以M为顶点的二次函数图象为![]() .
.
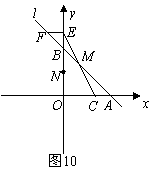
(1)当m=6时,①直接写出点M、F的坐标,
②求![]() 、
、![]() 的函数解析式;
的函数解析式;
(2)当m发生变化时,
①在![]() 的每一支上,y随x的增大如何变化?请说明理由.
的每一支上,y随x的增大如何变化?请说明理由.
②若![]() 、
、![]() 中的y都随着x的增大
中的y都随着x的增大![]() 而减小,写出x的取值范围.
而减小,写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,过反比例函数 ![]() 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,
图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E, ![]() 与梯形ECDB的面积分别为
与梯形ECDB的面积分别为 ![]() ,比较它们的大小,可得( )
,比较它们的大小,可得( )
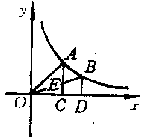
A. ![]() B.
B. ![]() C.
C. ![]() D. 大小关系不能确定
D. 大小关系不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com