
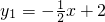 交x轴于A,该直线与抛物线
交x轴于A,该直线与抛物线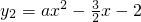 在第二象限内
在第二象限内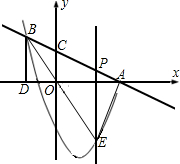 的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9.
的交点是B,BD⊥x轴,垂足为D,且△ABD的面积是9. x+2=0,
x+2=0, x+2,
x+2, (4-x)×(-
(4-x)×(- x+2)=9,
x+2)=9, x+2=-
x+2=- ×(-2)+2=3,
×(-2)+2=3,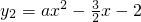 在第二象限内的交点是B,
在第二象限内的交点是B, ×(-2)-2=3,
×(-2)-2=3, ,
, x2-
x2- x-2;
x-2; x2-
x2- x-2;
x-2;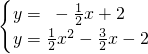 ,
,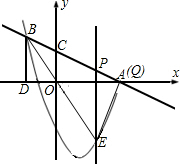
 ,
, ,
, m+2,
m+2, m2-
m2- m-2,
m-2, m+2)-(
m+2)-( m2-
m2- m-2)=-
m-2)=- m2+m+4;
m2+m+4; ×(-
×(- m2+m+4)×[m-(-2)]+
m2+m+4)×[m-(-2)]+ ×(-
×(- m2+m+4)×(4-m),
m2+m+4)×(4-m), ×(-
×(- m2+m+4)×(m+2+4-m),
m2+m+4)×(m+2+4-m), (m2-2m-8),
(m2-2m-8), (m-1)2+
(m-1)2+ ,
, <0,
<0, ,
, ×1+2=
×1+2= ,
, ).
).

科目:初中数学 来源:第3章《圆》中考题集(38):3.5 直线和圆的位置关系(解析版) 题型:解答题
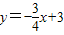 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
查看答案和解析>>
科目:初中数学 来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版) 题型:解答题
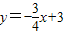 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.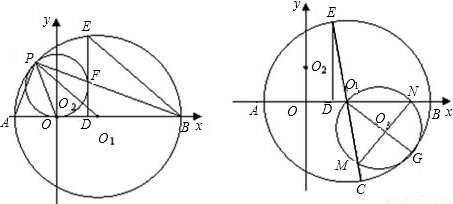
查看答案和解析>>
科目:初中数学 来源:第27章《相似》中考题集(15):27.2 相似三角形(解析版) 题型:解答题
 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省恩施州利川市东城初中九年级(上)入学选拔考试数学试卷(解析版) 题型:解答题
 交x轴于点A,交直线
交x轴于点A,交直线 于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
于点B(2,m).矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴的上方,DC=2,DE=4.当点C的坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(37):3.5 直线和圆的位置关系(解析版) 题型:解答题
 交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com