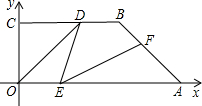
解:(1)∵OA=4

,AB=4,∠OAB=90°,
∴tan∠AOB=

,
∴∠AOB=30°,
∵OA=OH,OB=OB,∠BAO=∠BHO=90°,
∴Rt△AOB≌Rt△HOB(HL),
∴∠BOH=∠AOB=30°,
∴∠HOC=30°;
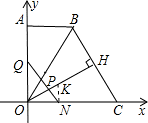
(2)①过点N与H作NK⊥x轴,
∴NK∥OA,
∴△POQ∽△PKN,
∴当

=

时,
∵OQ=4

-t,OP=t,
∴PK=

t,NK=

(4

-t),
∴OK=

t,
∵∠HOC=30°,
∴

,
∴t=
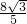
,
∴当t为
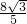
时,QP=2PN;
②

当QP⊥OH时,△OPQ∽△HOB.
∵∠QPO=∠OHB=90°,∠QOP=∠OBH=60°,
∴△OPQ∽△HOB,
∴cos∠QOP=

,
∴t=

,
∴当t=

时,△OPQ与△HOB相似.
③当PQ⊥OA时,△OPQ∽△BOH,
cos∠QOP=
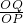
=

,
解得:t=

.
分析:(1)首先由三角函数,求得∠AOB的度数,由HL,可证得Rt△AOB≌Rt△HOB,即可求得∠HOC的度数;
(2)首先作辅助线:过点N与H作NK⊥x轴,即可得到相似三角形:△POQ∽△PKN,由相似三角形的对应边成比例,即可求得t的值;
(3)由相似三角形的判定,易得当QP⊥OH时,△OPQ∽△HOB,由三角函数的性质,即可求得当t=

时,△OPQ与△HOB相似.
点评:此题考查了相似三角形的判定与性质,以及三角函数的性质与全等三角形的判定与性质.题目综合性很强,难度比较大,解题时要注意仔细分析求解.

 ),B(4,4
),B(4,4 ),C(8,0),OH垂
),C(8,0),OH垂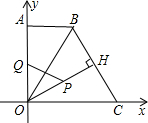 直BC于H,若OH=
直BC于H,若OH= .
. ,AB=4,∠OAB=90°,
,AB=4,∠OAB=90°, ,
,
 =
= 时,
时, -t,OP=t,
-t,OP=t, t,NK=
t,NK= (4
(4 -t),
-t), t,
t, ,
,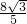 ,
,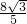 时,QP=2PN;
时,QP=2PN; 当QP⊥OH时,△OPQ∽△HOB.
当QP⊥OH时,△OPQ∽△HOB. ,
, ,
, 时,△OPQ与△HOB相似.
时,△OPQ与△HOB相似. =
= ,
, .
. 时,△OPQ与△HOB相似.
时,△OPQ与△HOB相似.


 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=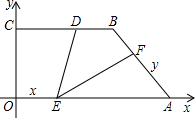 是BC上一点,BD=
是BC上一点,BD=