
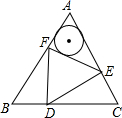
 已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为________.
已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为________.
 a2,S△DEF=
a2,S△DEF= b2,
b2, (S△ABC-S△DEF)=
(S△ABC-S△DEF)=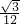 (a2-b2),
(a2-b2),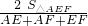 =
= (a-b)=
(a-b)= .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
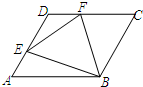 已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.
已知:如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,请你判断:无论E、F怎样移动,当满足:AE+CF=a时,△BEF是什么三角形?并说明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com