
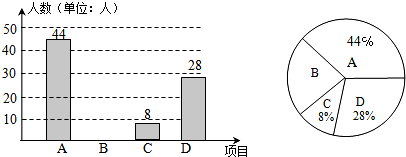
分析 (1)用1减去其它项目的百分比即可求得喜欢B项目的百分比,然后乘以360°即可求得对应的扇形圆心角的度数;
(2)根据喜欢C项目的有8人,所占的百分比是8%即可求得调查的总人数,进而求得喜欢B项目的人数,补全直方图;
(3)利用总人数1000乘以对应的百分比即可求解.
解答 解:(1)喜欢B项目的人数所占的百分比是:1-8%-28%-44%=20%,
对应的扇形圆心角度数是:360°×20%=72°.
故答案是:20%,72°;
(2)抽取的总人数是:8÷8%=100(人),
喜欢B项目的人数是:100×20%=20人, ;
;
(3)1000×28%=280(人).
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| X | -2 | -1 | 0 |
| y | 3 | 2 | 1 |
| A. | x>-1 | B. | x<1 | C. | x>-3 | D. | x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com