
分析 由于$\sqrt{{x}^{2}-2x+1}$=|x-1|,所以分两种情况进行讨论:①当x≥1时,|x-1|=x-1,原方程化为$\sqrt{{x}^{2}-3x+4}$=3;②当x<1时,|x-1|=1-x,原方程化为$\sqrt{{x}^{2}+x}$=3.分别把方程两边平方去根号后求解.
解答 解:∵$\sqrt{{x}^{2}-2x+1}$=|x-1|,
∴$\sqrt{{x}^{2}-x+2-2\sqrt{{x}^{2}-2x+1}}$=$\sqrt{{x}^{2}-x+2-2|x-1|}$.
分两种情况:①当x≥1时,|x-1|=x-1,
原方程可化为$\sqrt{{x}^{2}-3x+4}$=3,
两边平方得,x2-3x+4=9,
整理,得x2-3x-5=0,
∵△=9-4×1×(-5)=29,
∴x=$\frac{3±\sqrt{29}}{2}$,
x1=$\frac{3+\sqrt{29}}{2}$,x2=$\frac{3-\sqrt{29}}{2}$(不合题意舍去),
经检验,知x=$\frac{3+\sqrt{29}}{2}$是原方程的解;
②当x<1时,|x-1|=1-x,
原方程可化为$\sqrt{{x}^{2}+x}$=3,
两边平方得,x2+x=9,
整理,得x2+x-9=0,
∵△=1-4×1×(-9)=37,
∴x=$\frac{-1±\sqrt{37}}{2}$,
x1=$\frac{-1-\sqrt{37}}{2}$,x2=$\frac{-1+\sqrt{37}}{2}$(不合题意舍去),
经检验,知x=$\frac{-1-\sqrt{37}}{2}$是原方程的解.
∴方程$\sqrt{{x}^{2}-x+2-2\sqrt{{x}^{2}-2x+1}}$=3的所有实数的和为:$\frac{3+\sqrt{29}}{2}$+$\frac{-1-\sqrt{37}}{2}$=$\frac{2+\sqrt{29}-\sqrt{37}}{2}$.
故答案为$\frac{2+\sqrt{29}-\sqrt{37}}{2}$.
点评 本题考查了无理方程的解法.在解无理方程时最常用的方法是两边平方法及换元法,本题用了平方法.注意解无理方程一定要验根.进行分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
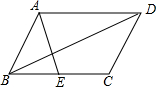 如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$.
如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( )| A. | 70° | B. | 65° | C. | 55° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com