
 如图,已知正方形ABCD的边长为2,以DC为底向正方形外作等腰△DEC,连接AE,以AE为腰作等腰△AEF,使得EA=EF,且∠DEC=∠AEF.
如图,已知正方形ABCD的边长为2,以DC为底向正方形外作等腰△DEC,连接AE,以AE为腰作等腰△AEF,使得EA=EF,且∠DEC=∠AEF.分析 (1)由等腰三角形的性质得出DE=CE,AE=FE,∠EDC=∠ECD=∠EAF=∠EFA,即可得出△EDC∽△EAF;
(2)由正方形的性质得出BC=DC=2,∠BCD=∠ADC=90°,∠ACB=∠ACD=45°,证出∠AED=∠FEC,由SAS证明△ADE≌△FCE,得出AD=FC,∠ADE=∠FCE=90°+∠EDC,证出BC=FC,∠BCF=∠DEC,得出△BCF∽△DEC,得出对应边成比例,即可得出答案;
(3)求出∠BCF=45°,由(2)得出∠DEC=∠BCF=45°即可.
解答 (1)证明:∵△DEC、△AEF是等腰三角形,且∠DEC=∠AEF,
∴DE=CE,AE=FE,∠EDC=∠ECD=∠EAF=∠EFA,
∴△EDC∽△EAF;
(2)解:∵四边形ABCD是正方形,
∴BC=DC=2,∠BCD=∠ADC=90°,∠ACB=∠ACD=45°,
∵∠DEC=∠AEF,
∴∠AED=∠FEC,
在△ADE和△FCE中,$\left\{\begin{array}{l}{DE=CE}&{\;}\\{∠AED=∠FEC}&{\;}\\{AE=FE}&{\;}\end{array}\right.$,
∴△ADE≌△FCE(SAS),
∴AD=FC,∠ADE=∠FCE=90°+∠EDC,
∴BC=FC,∠BCF=360°-∠BCE-∠FCE=360°-2(90°+∠ECD)=180°-2∠ECD=∠DEC,
又∵BC:DE=FC:CE,
∴△BCF∽△DEC,
∴$\frac{BC}{DE}=\frac{BF}{DC}$,
∴DE•BF=BC•DC=2×2=4;
(3)解:∵CF⊥AC,∠ACB=45°,
∴∠BCF=45°,
由(2)得:∠DEC=∠BCF=45°.
点评 本题是四边形综合题目,考查了正方形的性质、等腰三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:解答题
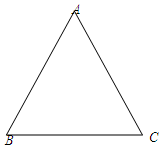 如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.
如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
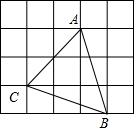 如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )
如图,网格中小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正弦值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段 | 频数 | 频率 |
| 72分以下 | 368 | 0.2 |
| 72----80分 | 460 | 0.25 |
| 81----95分 | 644 | 0.35 |
| 96----108分 | 184 | 0.2 |
| 109----119分 | 130 | |
| 120分 | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在150≤x<175之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:| 组别 | 身高(cm) |
| A | 150≤x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | 170≤x<175 |
| A. | ①② | B. | ①④ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线与x轴的两个交点分别为A(1,0),B(4,0)与y轴交于点C(0,4),点P为抛物线上的一个动点.
如图,抛物线与x轴的两个交点分别为A(1,0),B(4,0)与y轴交于点C(0,4),点P为抛物线上的一个动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com