
如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切与点D,与AB相交于点E。
(1)试判断AD是否平分∠BAC?并说明理由;
(2)若BD=3BE,CD=3,求?O的半径。
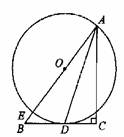
解:(1)判断:AD平分∠BAC,
证法一:连接OD.
∵BC切⊙O与D,∴OD⊥BC,又△ABC为Rt△,且∠C=90°.
∴AC⊥BC ∴OD∥AC ∴∠1=∠2 ∴∠1=∠3.
证法二,连接ED.
∴AE是⊙O直径,∴∠ADF=90°,∴∠3+∠AED=90°.又∠C=90°
∴∠1+∠ADC=90°.又∠AED=∠ADC ∴∠1=∠3.
证法三,连接EF,DF.
∵AE是⊙0直径,∴∠AFE=90°,又ACE=90°,∴∠AFE=∠ACB,∴EF∥BC,
∴∠4=∠5.又∠3=∠4,∠1=∠5,∴∠1=∠3
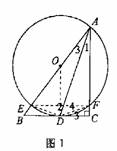
(2) 解法:设BE-x,则BD=3BE=3x.据切割线定理得 BD2=BE?BA.得AB-9x, OA=OE-4x.又OD∥AC,∴![]() ∴
∴![]() ∴
∴![]() ∴⊙O的半径为5.
∴⊙O的半径为5.
解法二:如图2,过O作OG⊥AC,又AC⊥BC,OD⊥BC,则四边形ODCG为矩形。
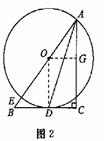
∴OG=CD=3,OG∥BC,又OG∥BC,∴![]() ∴
∴![]() ∴
∴![]() ,x=0(舍去)∴⊙O的半径为5.
,x=0(舍去)∴⊙O的半径为5.
备注:本解法是在解法一得AB=9x,OA=OE=4x的基础上进行的。
解法三:如图(1)∠3=∠BDE,∠EBD=∠DBA,∴![]() ,又BD=3BE,∴
,又BD=3BE,∴![]() .
.
又DC=3,则AC=9,在Rt△ADC中,AD=![]() ,在Rt△ AED中,AE=
,在Rt△ AED中,AE=![]() ∴⊙O的半径的长为
∴⊙O的半径的长为![]() .
.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
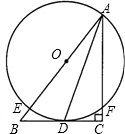
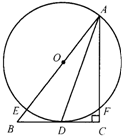 19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.
19、如图,已知点O为Rt△ABC斜边AB上一点,以O为圆心,OA为半径的圆与BC相切于点D,与AB相交于点E,与AC相交于点F.试判断AD是否平分∠BAC.并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
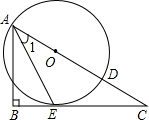 (2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2012•玉林)如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:
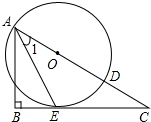 如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com