
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线
点的一条直线![]()
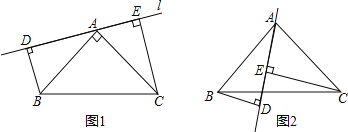
(1)作![]() 于点
于点![]() ,
,![]()
![]() 点,若
点,若![]() 点和
点和![]() 点在直线
点在直线![]() 的同侧,求证:
的同侧,求证:![]() ;
;
(2)若直线![]() 绕点
绕点![]() 旋转到
旋转到![]() 点和
点和![]() 点在其两侧,其余条件不变,问:
点在其两侧,其余条件不变,问:![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
【答案】(1)证明见解析;(2)CE=BD+DE,理由见解析;
【解析】
(1)由AAS证明△ABD≌△CAE,得到BD=AE,AD=CE,即可解决问题.
(2)由AAS证明证明△ABD≌△CAE,得出BD=AE,AD=CE,即可得出结论.
(1)证明:∵∠BAC=90°,BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=∠DAB+∠EAC,
∴∠DBA=∠EAC;
在△ABD与△CAE中,
 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴DE=BD+CE.
(2)解:CE=BD+DE;理由如下:
同(1)得:∠ABD=∠CAE,
在△ABD和△CAE中,
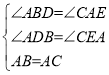 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD=AE+DE,
∴CE=BD+DE.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.
(1)若∠ABC=70°,则∠NMA的度数是 度.
(2)若AB=8cm,△MBC的周长是14cm.
①求BC的长度;
②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=10,E为AB上一点,且AE= ![]() AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.
AB=a,连结DE,F是DE中点,连结BF,以BF为直径作⊙O.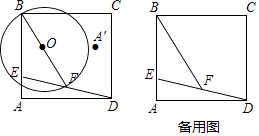
(1)用a的代数式表示DE2= , BF2=;
(2)求证:⊙O必过BC的中点;
(3)若⊙O与矩形ABCD各边所在的直线相切时,求a的值;
(4)作A关于直线BF的对称点A′,若A′落在矩形ABCD内部(不包括边界),则a的取值范围 . (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
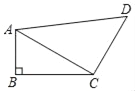
【题目】如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】凤凰景区的团体门票的价格规定如下表
购票人数 | 1~55 | 56~110 | 111~165 | 165以上 |
价格(元/人) | 10 | 9 | 8 | 7 |
某校七年级(1)班和(2)班共112人去凤凰景区进行研学春游活动,当两班都以班为单位分别购票,则一共需付门票1060元.
(1)你认为由更省钱的购票方式吗?如果有,能节省多少元?
(2)若(1)班人数多于(2)班人数,求(1)(2)班的人数各是多少?
(3)若七年级(3)班53人也一同前去春游时,如何购票显得更为合理?请你设计一种更省钱的方案,并求出七年级3个班共需付门票多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣(2m+1)x+2m不经过第三象限,且当x>2时,函数值y随x的增大而增大,则实数m的取值范围是( )
A.0≤m≤1.5
B.m≥1.5
C.0≤m≤1
D.0<m≤1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.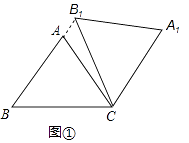
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.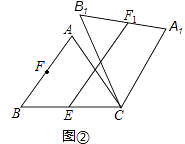
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
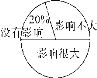
人数统计表如下:
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com