
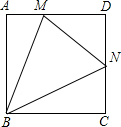
 如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值.
如图,在正方形ABCD中,N是DC的中点,M是AD上异于点D的点,且∠NMB=∠MBC,求$\frac{AM}{AB}$的值. 分析 根据∠NMB=∠MBC,延长MN,BC相交于T,得到等腰△TBM,连接点T和MB的中点,得到相似三角形,然后由相似三角形的性质进行计算,求出∠ABM的正切,即AM:AB的值.
解答 解:如图:延长MN交BC的延长线于T,设MB的中点为O,连TO,则OT⊥BM,
∵∠ABM+∠MBT=90°,
∠OTB+∠MBT=90°,
∴∠ABM=∠OTB,则△BAM∽△TOB,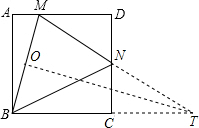
∴$\frac{AM}{MB}=\frac{OB}{BT}$,
即MB2=2AM•BT ①,
令DN=1,CT=MD=K,则:AM=2-K,BM=$\sqrt{4+(2-K)^{2}}$,BT=2+K,
代入①中得:4+(2-K)2=2(2-K)(2+K),
解方程得:K1=0(舍去),K2=$\frac{4}{3}$.
∴AM=2-$\frac{4}{3}$=$\frac{2}{3}$.
∴tan∠ABM=$\frac{AM}{AB}$=$\frac{1}{3}$.
点评 本题考查的是解直角三角形,运用正方形的性质,根据题目中角的关系,判断两个三角形相似,然后用相似三角形的性质进行计算,求出直角三角形中边的长度,再用正切的定义求出角的正切值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
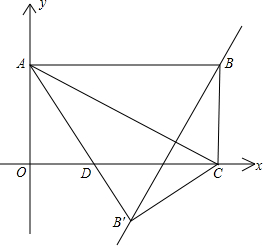 如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足:|OA-2|+OC2-4$\sqrt{3}$•OC+12=0.
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足:|OA-2|+OC2-4$\sqrt{3}$•OC+12=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )
在矩形ABCD中,AB=3,BC=1,E在AB上,AE=2,分别以E、B为圆心,以AE长为半径,画圆弧交DC于F、G,现向矩形ABCD区域内做投针试验,则投中阴影区域的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com