练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    正方形的两条对角线之和为8cm，则其面积为


    1. A.
      数学公式cm2
    2. B.
      16cm2
    3. C.
      8cm2
    4. D.
      4cm2
    C
    分析：根据正方形的对角线相等且互相垂直，正方形是特殊的菱形，菱形的面积等于对角线乘积的一半进行求解即可．
    解答：∵正方形的两条对角线之和为8cm，正方形的对角线相等，
    ∴正方形的一条对角线长为4cm，
    ∴面积是 ×4×4=8cm2．
    故选C．
    点评：本题考查了正方形的对角线相等，且互相垂直的性质，菱形的面积的求解，本题也可以先求出正方形的边长，再利用正方形的面积等于边长的平方求解，但稍比较麻烦．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2011-2012学年山东威海市八年级下期末模拟数学试卷（三）（带解析） 题型：解答题

    某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD（AB＜BC）的对角线的交点O旋转（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
    ⑴该学习小组成员意外的发现图①（三角板一直角边与OD重合）中，BN2=CD2+CN2，在图③中（三角板一边与OC重合），CN2=BN2+CD2，请你对这名成员在图①和图③中发现的结论选择其一说明理由。

    ⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系，写出你的结论，并说明理由。

    ⑶将矩形ABCD改为边长为1的正方形ABCD，直角三角板的直角顶点绕O点旋转到图④，两直角边与AB、BC分别交于M、N，直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系（不需要证明）

    查看答案和解析>>

    科目：初中数学 来源：2013届山东威海市八年级下期末模拟数学试卷（三）（解析版） 题型：解答题

    某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD（AB＜BC）的对角线的交点O旋转（①→②→③），图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。

    ⑴该学习小组成员意外的发现图①（三角板一直角边与OD重合）中，BN2=CD2+CN2，在图③中（三角板一边与OC重合），CN2=BN2+CD2，请你对这名成员在图①和图③中发现的结论选择其一说明理由。

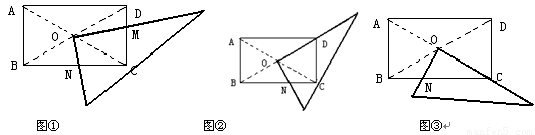
    ⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系，写出你的结论，并说明理由。

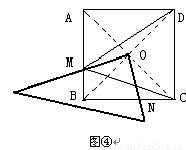
    ⑶将矩形ABCD改为边长为1的正方形ABCD，直角三角板的直角顶点绕O点旋转到图④，两直角边与AB、BC分别交于M、N，直接写出BN、CN、CM、DM这四条线段之  间所满足的数量关系（不需要证明）

     

    查看答案和解析>>

    同步练习册答案