

 ,
,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:在△AOB中,AB=4
已知:在△AOB中,AB=4| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年北京市门头沟区中考二模数学试卷(带解析) 题型:解答题
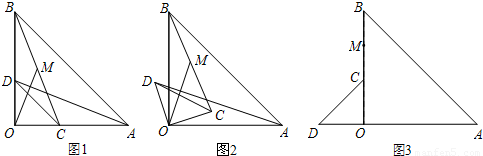
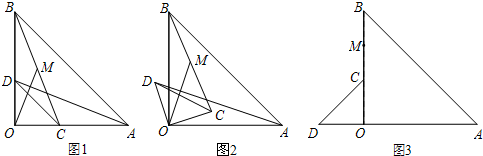
已知:在△AOB与△COD中,OA=OB,OC=OD, .
.
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则线段AD与OM之间的数量关系是 ,位置关系是 ;
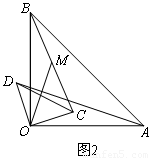
(2)如图2,将图1中的△COD绕点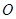 逆时针旋转,旋转角为
逆时针旋转,旋转角为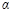 (
(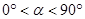 ).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
(3)如图3,将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.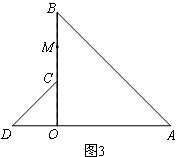
请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2013年北京市门头沟区中考二模数学试卷(解析版) 题型:解答题
已知:在△AOB与△COD中,OA=OB,OC=OD,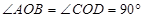 .
.
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则线段AD与OM之间的数量关系是 ,位置关系是 ;
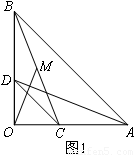
(2)如图2,将图1中的△COD绕点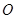 逆时针旋转,旋转角为
逆时针旋转,旋转角为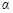 (
(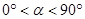 ).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的两个结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
(3)如图3,将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.
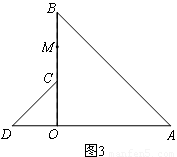
请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com