
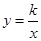 图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=
图象上的点,其中x1=1、x2=2、…、xn=n.记T1=x1·y2、T2=x2·y3、…、T2012=x2012·y2013.若T1=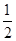 ,则T1·T2·…·T2012=【 】
,则T1·T2·…·T2012=【 】A.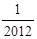 | B.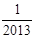 | C.2012 | D.2013 |
科目:初中数学 来源:不详 题型:解答题
 的图象上,AC⊥x轴,垂足为C,且△AOC的面积为
的图象上,AC⊥x轴,垂足为C,且△AOC的面积为 .(1)求反比例函数的解析式;
.(1)求反比例函数的解析式;
 ,过点A的直线交x、y轴于E、F两点,且△EOF以点A为外心,求这条直线的解析式;
,过点A的直线交x、y轴于E、F两点,且△EOF以点A为外心,求这条直线的解析式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
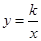 (
(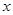 >0)的图象上的一点,PN垂直
>0)的图象上的一点,PN垂直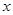 轴于点N,PM
轴于点N,PM 的图象经过点P.
的图象经过点P.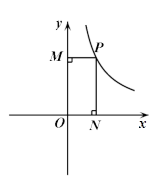
 与
与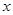 轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的
轴的交点为A,点Q在y轴上,当△QOA的面积等于矩形OMPN的面积的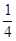 时,直接写出点Q的坐标.
时,直接写出点Q的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
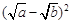 ≥0, ∴
≥0, ∴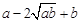 ≥0,∴
≥0,∴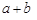 ≥
≥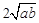
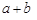 ≥
≥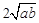 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥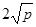 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值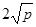 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题: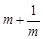 有最小值 ;
有最小值 ;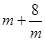 有最小值 .
有最小值 .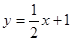 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线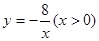 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.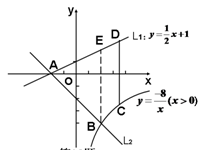
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象交于M、N两点.
的图象交于M、N两点.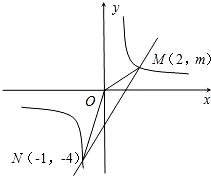
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com