

���� ��1�����ݹ��ɶ����ó�AC�ij��ȣ��ٸ��ݱ����֮��Ĺ�ϵ���ɵó����ۣ�
��2������D��DM��EF�ڵ�M��������ȵı߽ǹ�ϵ֤����DEM�ա�EAH��AAS�����ɴ˼��ɵó�DM=EH��EM=AH����ͨ���ǵļ����ҳ���AHG����DMG��Ϊ����ֱ�������Σ����ݵ���ֱ�������ε�б����ֱ�DZߵĹ�ϵ����֤��DG+AG=$\sqrt{2}$EG��
��3����ACΪֱ����Բ���ӳ�MN��Q��ʹ��MQ=AM������AQ�����ݡ�AMC=��ABC=90�㣬�ɵó���B��M��Բ�ϣ�����Բ�ܽǶ������ɵó���AMB=��ACB=45�㣬�ɡ�AMN=90�㣬AM=MQ�ɵó���AMQΪ����ֱ�������Σ������ó���AQM=45��=��AMB����ͨ���ǵļ���ó���BAM=��CAQ���ɴ˼��ɵó���BAM�ס�CAQ���������������ε����ʼ��ɵó�$\frac{BM}{CM+AM}$=$\frac{\sqrt{2}}{2}$��
��� ��1���⣺�ߵ���ֱ��������ABC�У�AB=AF=2$\sqrt{2}$��
��AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4��
��CF=AC-AF=4-2$\sqrt{2}$��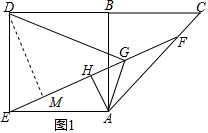 ��2��֤������ͼ1������D��DM��EF�ڵ�M��
��2��֤������ͼ1������D��DM��EF�ڵ�M��
���EDM+��DEM=90�㣬
�ߡ�DEM+��AEH=90�㣬
���EDM=��AEH��
��AH��EF��
���AHE=��DME=90�㣬��FAH=$\frac{1}{2}$��EAF=$\frac{1}{2}$����90��+45�㣩=67.5�㣬
�ڡ�DEM�͡�EAH�У�
$\left\{\begin{array}{l}{��EDM=��AEH}\\{��DME=��EHA}\\{DE=EA}\end{array}\right.$��
���DEM�ա�EAH��AAS����
��DM=EH��EM=AH��
��AGƽ�֡�BAC��
���FAG=$\frac{1}{2}$��BAC=22.5�㣬
���HAG=��FAH-��FAG=45�㣬
���AHG�ǵ���ֱ�������Σ�
��AH=HG��AG=$\sqrt{2}$AH=$\sqrt{2}$EM��
��EM=HG��
��EH=GM��
��DM=MG��
����DMG�ǵ���ֱ�������Σ�
��DG=$\sqrt{2}$MG��
��DG+AG=$\sqrt{2}$GM+$\sqrt{2}$EM=$\sqrt{2}$��GM+EM��=$\sqrt{2}$EG��
��3���⣺��ͼ2����ACΪֱ����Բ���ӳ�MN��Q��ʹ��MQ=AM������AQ��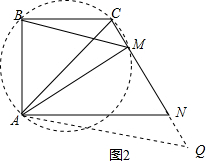
��AM��CN����ABCΪ����ֱ�������Σ�
���AMC=��AMN=90�㣬��ABC=90�㣬
���B��M��Բ�ϣ�
���AMB=��ACB=45�㣮
�ߡ�AMN=90�㣬AM=MQ��
���AMQΪ����ֱ�������Σ�
���AQM=45��=��AMB��
�֡ߡ�BAM=��BAC+��CAM=45��+��CAM����CAQ=��CAM+��MAQ=��CAM+45�㣬
���BAM=��CAQ��
���BAM�ס�CAQ��
��$\frac{BM}{CQ}=\frac{BA}{CA}$=$\frac{\sqrt{2}}{2}$��
��CQ=CM+MQ=CM+AM��
��$\frac{BM}{CM+AM}$=$\frac{\sqrt{2}}{2}$��
���� ���⿼���˹��ɶ���������ֱ�������ε����ʡ�Բ�ܽǶ����Լ����������ε��ж������ʣ�����Ĺؼ��ǣ���1�����ݹ��ɶ������AC�ij��ȣ���2�����ݵ���ֱ�������ε������ҳ�DG+AG=$\sqrt{2}$GM+$\sqrt{2}$EM=$\sqrt{2}$��GM+EM��=$\sqrt{2}$EG����3���������������ε������ҳ�������ϵʽ�������������⣬�����϶��֪ʶ�㣬�����������Ŀʱ����������ֱ���������Լ�Բ�����õ���ֱ�������ε������ҳ�����ߵĹ�ϵ�Լ�����Բ�ܽǶ����ҳ���ȵĽ��ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С��������ѧ��ȤС�飬�ƻ��ó߹���ͼ��ֱ�������Σ������ֱ�������ε�һ����Ϊ2���ĵ�λ���ȣ���һ����Ϊ4���ĵ�λ���ȣ�
С��������ѧ��ȤС�飬�ƻ��ó߹���ͼ��ֱ�������Σ������ֱ�������ε�һ����Ϊ2���ĵ�λ���ȣ���һ����Ϊ4���ĵ�λ���ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����AOB=��COD=90�㣬OEƽ�֡�BOD������AOD����BOC=5��1�����COE�Ķ���Ϊ��������
��ͼ����AOB=��COD=90�㣬OEƽ�֡�BOD������AOD����BOC=5��1�����COE�Ķ���Ϊ��������| A�� | 30�� | B�� | 40�� | C�� | 50�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼB����A������ƫ��45�㷽��C����A������ƫ��15�㷽��C����B��ƫ��80�㷽�����ACB=85�㣮
��ͼB����A������ƫ��45�㷽��C����A������ƫ��15�㷽��C����B��ƫ��80�㷽�����ACB=85�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.3��0.4��0.5 | B�� | 1��$\sqrt{2}$��$\sqrt{3}$ | C�� | 3��5��6 | D�� | 5��12��13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
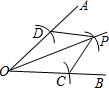 ��ͼ���ó߹���ͼ����ƽ���ߣ���OΪԲ�ģ����ⳤΪ�뾶������OA��OB�ڵ�C��D���ٷֱ���C��DΪԲ�ģ��Դ���$\frac{1}{2}CD$��Ϊ�뾶�������������ڵ�P���ɴ˵á�POC�ա�POD�����ǣ�������
��ͼ���ó߹���ͼ����ƽ���ߣ���OΪԲ�ģ����ⳤΪ�뾶������OA��OB�ڵ�C��D���ٷֱ���C��DΪԲ�ģ��Դ���$\frac{1}{2}CD$��Ϊ�뾶�������������ڵ�P���ɴ˵á�POC�ա�POD�����ǣ�������| A�� | AAS | B�� | SAS | C�� | SSS | D�� | ASA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com