
 如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=
如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH= BC;④FH2=HE•HB,正确的是
BC;④FH2=HE•HB,正确的是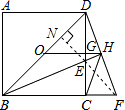 解:作EN⊥BD于N,连接EF.
解:作EN⊥BD于N,连接EF.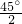 =22.5°
=22.5° CF=
CF= CE,CE<CG=
CE,CE<CG= BC,即CE<
BC,即CE< BC.
BC.

 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
 如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=
如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=| 1 |
| 4 |
| A、①②③ | B、②③④ |
| C、①②④ | D、①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:第24章《相似形》中考题集(07):24.3 相似三角形的性质(解析版) 题型:选择题
 BC;④FH2=HE•HB,正确的是( )
BC;④FH2=HE•HB,正确的是( )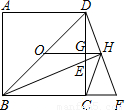
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com