
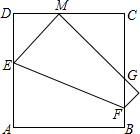
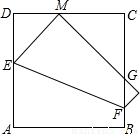
 小丽将一个边长为2a的正方形纸片ABCD折叠,顶点A落到CD边上的点M的位置,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).在折叠过程中,小丽发现当点M在CD边上的任意位置时,(点C,D除外),△CMG的周长总是相等的,那么△CMG的周长为________.
小丽将一个边长为2a的正方形纸片ABCD折叠,顶点A落到CD边上的点M的位置,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).在折叠过程中,小丽发现当点M在CD边上的任意位置时,(点C,D除外),△CMG的周长总是相等的,那么△CMG的周长为________.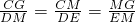 ,即
,即 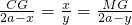
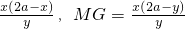
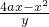
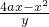 =
=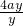 =4a.
=4a.

科目:初中数学 来源: 题型:
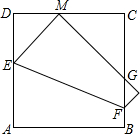 小丽将一个边长为2a的正方形纸片ABCD折叠,顶点A落到CD边上的点M的位置,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).在折叠过程中,小丽发现当点M在CD边上的任意位置时,(点C,D除外),△CMG的周长总是相等的,那么△CMG的周长为
小丽将一个边长为2a的正方形纸片ABCD折叠,顶点A落到CD边上的点M的位置,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).在折叠过程中,小丽发现当点M在CD边上的任意位置时,(点C,D除外),△CMG的周长总是相等的,那么△CMG的周长为查看答案和解析>>
科目:初中数学 来源:2007年第5届“学用杯”全国数学知识应用竞赛九年级初赛试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com