
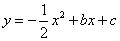 与x轴交于A(1,0)、
与x轴交于A(1,0)、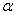 (0°<
(0°<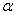 <90°)
<90°)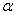 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?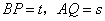 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.
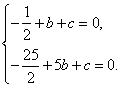 解得
解得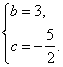 ……………(2分)
……………(2分)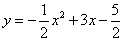 =
=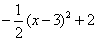 ∴顶点C的坐标为(3,2).……………(3分)
∴顶点C的坐标为(3,2).……………(3分)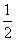 ∠PCQ=22.5°.
∠PCQ=22.5°.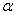 =22.5°时,△CPQ是等腰三角形.……………(5分)
=22.5°时,△CPQ是等腰三角形.……………(5分)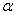 =45°时,△CPQ是等腰三角形.……………(6分)
=45°时,△CPQ是等腰三角形.……………(6分)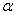 =0°,不合题意.
=0°,不合题意. 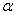 =22.5°或45°时,△CPQ是等腰三角形.………(7分)
=22.5°或45°时,△CPQ是等腰三角形.………(7分)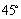 ,
,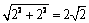 ……………(8分)
……………(8分)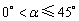 时,∵∠ACQ=∠ACP+∠PCQ=∠ACP+45°.
时,∵∠ACQ=∠ACP+∠PCQ=∠ACP+45°.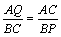 .∴AQ·BP=AC·BC=
.∴AQ·BP=AC·BC=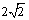 ×
×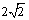 ="8" ……………(9分)
="8" ……………(9分)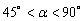 时,同理可得AQ·BP=AC·BC="8 " ∴
时,同理可得AQ·BP=AC·BC="8 " ∴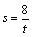 .……………(10分)
.……………(10分)

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:不详 题型:单选题
| A.这个图形一定是中心对称图形 | B.这个图形可能是中心对称图形 |
| C.这个图形旋转216°后能与它本身重合 | D.以上都不对 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, ,
, ,
, .等腰直角三角形
.等腰直角三角形 的斜边
的斜边 ,
, 点与
点与 点重合,
点重合, 和
和 在一条直线上,设等腰梯形
在一条直线上,设等腰梯形 不动,等腰直角三角形
不动,等腰直角三角形 沿
沿 所在直线以
所在直线以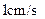 的速度向右移动,直到点
的速度向右移动,直到点 与点
与点 重合为止.
重合为止. 在整个移动过程中与等腰梯形
在整个移动过程中与等腰梯形 重叠部分的形状由 形
重叠部分的形状由 形 移动
移动 时,等腰直角三角形
时,等腰直角三角形 与等腰梯形
与等腰梯形 重
重 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式; 时,求等腰直角三角形
时,求等腰直角三角形 与等腰梯形
与等腰梯形 重叠部分的面积.
重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.矩形 | B.菱形 | C.正方形 | D.梯形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
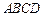 中,点F在边BC上,E在边BA的延长线上.
中,点F在边BC上,E在边BA的延长线上.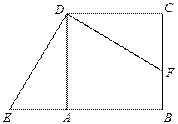
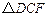 按顺时针方向旋转后恰好与
按顺时针方向旋转后恰好与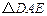 重合.则旋转
重合.则旋转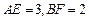 ,求四边形
,求四边形 的面积.
的面积. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com