
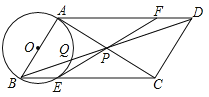
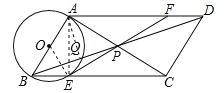
【题目】如图,在ABCD中,∠BAC=90°,对角线AC,BD相交于点P,以AB为直径的⊙O分别交BC,BD于点E,Q,连接EP并延长交AD于点F.
(1)求证:EF是⊙O的切线;
(2)求证:![]() =4BPQP.
=4BPQP.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)连接OE,AE,由AB是⊙O的直径,得到∠AEB=∠AEC=90°,根据四边形ABCD是平行四边形,得到PA=PC推出∠OEP=∠OAC=90°,根据切线的判定定理即可得到结论;
(2)由AB是⊙O的直径,得到∠AQB=90°根据相似三角形的性质得到![]() =PBPQ,根据全等三角形的性质得到PF=PE,求得PA=PE=
=PBPQ,根据全等三角形的性质得到PF=PE,求得PA=PE=![]() EF,等量代换即可得到结论.
EF,等量代换即可得到结论.
试题解析:(1)连接OE,AE,∵AB是⊙O的直径,∴∠AEB=∠AEC=90°,∵四边形ABCD是平行四边形,∴PA=PC,∴PA=PC=PE,∴∠PAE=∠PEA,∵OA=OE,∴∠OAE=∠OEA,∴∠OEP=∠OAC=90°,∴EF是⊙O的切线;
(2)∵AB是⊙O的直径,∴∠AQB=90°,∴△APQ∽△BPA,∴![]() ,∴
,∴![]() =PBPQ,在△AFP与△CEP中,∵∠PAF=∠PCE,∠APF=∠CPE,PA=PC,∴△AFP≌△CEP,∴PF=PE,∴PA=PE=
=PBPQ,在△AFP与△CEP中,∵∠PAF=∠PCE,∠APF=∠CPE,PA=PC,∴△AFP≌△CEP,∴PF=PE,∴PA=PE=![]() EF,∴
EF,∴![]() =4BPQP.
=4BPQP.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】用两块角度分别为30°、60°、90°和45°、45°、90°的三角板画角,不可能画出的角是( )
A. 125° B. 105° C. 75° D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2+8x﹣9=0时,此方程可变形为( )
A. (x+4)2=7 B. (x+4)2=25 C. (x+4)2=9 D. (x+4)2=﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A. y=(x+1)2+4 B. y=(x﹣1)2+4
C. y=(x+1)2+2 D. y=(x﹣1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=kx2﹣2x﹣1与x轴有两个不同的交点,则k的取值范围为( )
A. k>﹣1 B. k≥﹣1 C. k>﹣1 且 k≠0 D. k≥﹣1 且 k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列分解因式正确的是( )
A.2x2﹣xy=2x(x﹣y)
B.﹣xy2+2xy﹣y=﹣y(xy﹣2x)
C.2x2﹣8x+8=2(x﹣2)2
D.x2﹣x﹣3=x(x﹣1)﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com