
 如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.
如图,在⊙O中,AD、BC相交于点E,OE平分∠AEC.
 =
= ,
, -
- =
= -
- ,即
,即 ,
, =
= ,然后可得
,然后可得 =
= ,继而得出结论.
,继而得出结论.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
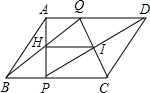 如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度?
如图,在?ABCD中,AD=6cm,点P、Q分别是边BC、AD上的动点,点P以一定的速度沿BC从B向C匀速运动,与此同时点Q以相同的速度沿AD从A向D运动,连接AP、PD、BQ、CQ、AP、BQ交于点H,PD、CQ交于点I,连接HI.试猜想:在运动的过程中,HI的长度是否变化?若变化,请说明理由;若不变,请求出HI的长度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com