
 的两个解是
的两个解是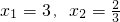 ;
; 的两个解是
的两个解是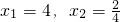 ;
; 的两个解是
的两个解是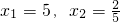 ;
;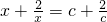 的两个解是
的两个解是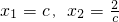 ;并且小王在老师的帮助下完成了严谨的证明(证明过程略).小王非常高兴,他向同学提出如下的问题.
;并且小王在老师的帮助下完成了严谨的证明(证明过程略).小王非常高兴,他向同学提出如下的问题.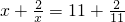 的两个解是x1=______和x2=______;
的两个解是x1=______和x2=______;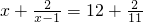 ,则x的两个解是多少?
,则x的两个解是多少?科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .
. 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.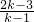 =0,解得k=
=0,解得k= .
. 是
是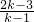 =0的解.
=0的解. 时,方程的两实数根x1,x2互为相反数.
时,方程的两实数根x1,x2互为相反数.查看答案和解析>>
科目:初中数学 来源:《第2章 一元二次方程》2010年创新题(解析版) 题型:解答题
 .
. 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.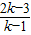 =0,解得k=
=0,解得k= .
. 是
是 =0的解.
=0的解. 时,方程的两实数根x1,x2互为相反数.
时,方程的两实数根x1,x2互为相反数.查看答案和解析>>
科目:初中数学 来源:《第23章 一元二次方程》2009年单元测试卷(解析版) 题型:解答题
 .
. 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根. =0,解得k=
=0,解得k= .
. 是
是 =0的解.
=0的解. 时,方程的两实数根x1,x2互为相反数.
时,方程的两实数根x1,x2互为相反数.查看答案和解析>>
科目:初中数学 来源:2003年山东省潍坊市中考数学试卷(解析版) 题型:解答题
 .
. 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根. =0,解得k=
=0,解得k= .
. 是
是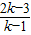 =0的解.
=0的解. 时,方程的两实数根x1,x2互为相反数.
时,方程的两实数根x1,x2互为相反数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com