
已知抛物线的顶点为P(-4,- ),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0)
),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0)

(1)求这条抛物线的函数关系式;
(2)若抛物线的对称轴交x轴于点D,则在线段AC上是否存在这样的点Q,使得△ADQ为等腰三角形?若存在,请求出符合条件的点Q的坐标;若不存在,请说明理由.
y=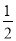 x2+4x-
x2+4x-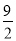 ;存在点Q1(-1,-4),Q2(2
;存在点Q1(-1,-4),Q2(2 -9,-
-9,- ),Q3(-
),Q3(-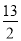 ,-
,-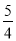 ).
).
【解析】
试题分析:(1)根据顶点坐标把抛物线设为顶点式形式y=a(x+4)2-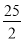 ,然后把点B的坐标代入解析式求出a的值,即可得解;
,然后把点B的坐标代入解析式求出a的值,即可得解;
(2)先根据顶点坐标求出点D的坐标,再根据抛物线解析式求出点A、C的坐标,从而得到OA、OC、AD的长度,根据勾股定理列式求出AC的长度,然后根据锐角三角形函数求出∠OAC的正弦值与余弦值,再分①AD=Q1D时,过Q1作Q1E1⊥x轴于点E1,根据等腰三角形三线合一的性质求出AQ1,再利用∠OAC的正弦求出Q1E1的长度,根据∠OAC的余弦求出AE1的长度,然后求出OE1,从而得到点Q1的坐标;②AD=AQ2时,过Q2作Q2E2⊥x轴于点E2,利用∠OAC的正弦求出Q2E2的长度,根据∠OAC的余弦求出AE2的长度,然后求出OE2,从而得到点Q2的坐标;③AQ3=DQ3时,过Q3作Q3E3⊥x轴于点E3,根据等腰三角形三线合一的性质求出AE3的长度,然后求出OE3,再由相似三角形对应边成比例列式求出Q3E3的长度,从而得到点Q3的坐标.
试题解析:(1)∵抛物线顶点坐标为(-4,-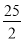 ),
),
∴设抛物线解析式为y=a(x+4)2-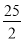
∵抛物线过点B(1,0),
∴a(1+4)2-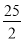 =0,
=0,
解得a=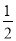 ,
,
所以,抛物线解析式为y=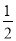 (x+4)2-
(x+4)2-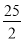 ,
,
即y=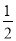 x2+4x-
x2+4x-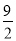 ;
;
(2)存在点Q1(-1,-4),Q2(2 -9,-
-9,- ),Q3(-
),Q3(-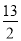 ,-
,-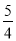 ).
).
理由如下:∵抛物线顶点坐标为(-4,-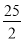 ),
),
∴点D的坐标为(-4,0),
令x=0,则y=-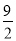 ,
,
令y=0,则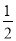 x2+4x-
x2+4x-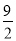 =0,
=0,
整理得,x2+8x-9=0,
解得x1=1,x2=-9,
∴点A(-9,0),C(0,-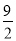 ),
),
∴OA=9,OC=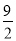 ,AD=-4-(-9)=-4+9=5,
,AD=-4-(-9)=-4+9=5,
在Rt△AOC中,根据勾股定理,AC=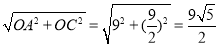
∴sin∠OAC=
cos∠OAC= ,
,
①AD=Q1D时,过Q1作Q1E1⊥x轴于点E1,
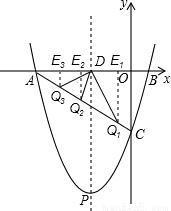
根据等腰三角形三线合一的性质,AQ1=2•ADcos∠OAC=2×5×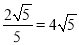 ,
,
Q1E1=AQ1•sin∠OAC=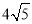 ×
×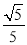 =4,
=4,
AE1=AQ1•cos∠OAC=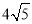 ×
×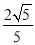 =8,
=8,
所以,OE1=OA-AE1=9-8=1,
所以,点Q1的坐标为(-1,-4);
②AD=AQ2时,过Q2作Q2E2⊥x轴于点E2,
Q2E2=AQ2•sin∠OAC=5×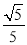 =
=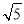 ,
,
AE2=AQ2•cos∠OAC=5×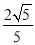 =2
=2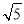 ,
,
所以,OE2=OA-AE2=9-2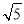 ,
,
所以,点Q2的坐标为(2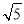 -9,-
-9,-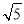 );
);
③AQ3=DQ3时,过Q3作Q3E3⊥x轴于点E3,
则AE3=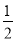 AD=
AD=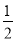 ×5=
×5=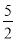 ,
,
所以,OE3=9- =
=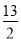 ,
,
∵Q3E3⊥x轴,OC⊥OA,
∴△AQ3E3∽△ACO,
∴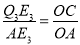 ,
,
即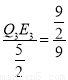 ,
,
解得Q3E3=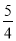 ,
,
所以,点Q3的坐标为(-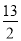 ,-
,-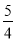 ),
),
综上所述,在线段AC上存在点Q1(-1,-4),Q2(2 -9,-
-9,- ),Q3(-
),Q3(-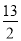 ,-
,-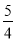 ),使得△ADQ为等腰三角形.
),使得△ADQ为等腰三角形.
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,已知:MN∥DC,∠ABE=130°,∠CDE=40°,求证:AB⊥MN。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图:∠1=∠2,则下列结论一定成立的是
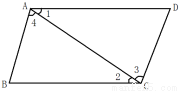
A、AB∥CD B、AD∥BC C、∠B=∠D D、∠3=∠4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:填空题
如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,则直线EF与BC的位置关系是 。
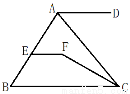
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市九年级上期末考试模拟考试数学试卷(解析版) 题型:解答题
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2)

(1)求m的值和抛物线的关系式;
(2)求不等式x2+bx+c>x+m的解集(直接写出答案).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市九年级上期末考试模拟考试数学试卷(解析版) 题型:填空题
若一个边长为a的正多边形的内角和等于720°,则这个正多边形的外接圆与内切圆的面积的比是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:选择题
如图,在△ABC中,DE∥BC,AD=3,BD=2,则△ADE与四边形DBCE的面积比是 ( )
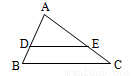
(A)3︰2; (B)3︰5; (C)9︰16; (D)9︰4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com