
【题目】如图,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA,劣弧 ![]() 的弧长为 . (结果保留π)
的弧长为 . (结果保留π) 
【答案】![]() π
π
【解析】解:连接OB,OC, ∵AB为圆O的切线,
∴∠ABO=90°,
在Rt△ABO中,OA=2,∠OAB=30°,
∴OB=1,∠AOB=60°,
∵BC∥OA,
∴∠OBC=∠AOB=60°,
又OB=OC,
∴△BOC为等边三角形,
∴∠BOC=60°,
则劣弧 ![]() 长为
长为 ![]() =
= ![]() π.
π.
故答案为: ![]() π
π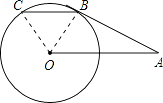
连接OB,OC,由AB为圆的切线,利用切线的性质得到三角形AOB为直角三角形,根据30度所对的直角边等于斜边的一半,由OA求出OB的长,且∠AOB为60度,再由BC与OA平行,利用两直线平行内错角相等得到∠OBC为60度,又OB=OC,得到三角形BOC为等边三角形,确定出∠BOC为60度,利用弧长公式即可求出劣弧BC的长.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(﹣1,0)和点B,与反比例函数y= ![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n). 
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= ![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 
(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣3x+m=0的两实数根是( )
A.x1=1,x2=﹣1
B.x1=1,x2=2
C.x1=1,x2=0
D.x1=1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 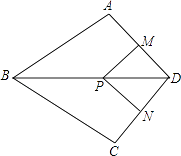
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC. 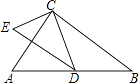
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com