(1)证明:设点A、B的坐标分别为(x
1,y
1)(x
2,y
2),
联立
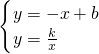
得,x
2-bx+k=0,
∴x
1•x
2=k,
又∵点A、B都在双曲线y=

上,
∴x
1•y
1=k,x
2•y
2=k,
∴x
1=y
2,x
2=y
1,
即AM=BN,OM=ON,
∵AM⊥y轴于M.BN⊥x轴于N,
∴∠AMO=∠BNO=90°,
在△AOM和△BON中,
∵
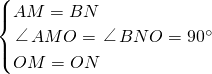
,
∴△AOM≌△BON(SAS),
∴OA=OB,
即:①OA=OB;②△AOM≌△BON;
(2)解:①如图,过O作OC⊥AB于点C,
∵OA=OB,∠AOB=45°,
∴∠AOC=∠BOC=22.5°,
∵△AOM≌△BON(已证),
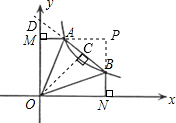
∴∠AOM=∠BON=

(90°-45°)=22.5°,
∴△AOM≌△AOC≌△BOC≌△BON(AAS),
∴S
△AOB=S
△AOM+S
△BON,
∵S
△AOM=

x
1•y
1=

k,S
△BON=

x
2•y
2=

k,
∴S
△AOB=

k+

k=k;
②如图,设直线AB与y轴的交点为D,
∵b=2,
∴当x=0时,y=-0+b=b=2,
∴点D的坐标为(0,2),
∴OD=2,
又∵∠COD=22.5°×2=45°,OC⊥AB,
∴OC=

×2=

,
∴OM=ON=

,
∴点P的坐标为(

,

).
分析:(1)设点A、B的坐标分别为(x
1,y
1)(x
2,y
2),联立两函数解析式整理得到关于x的一元二次方程,再根据反比例函数的性质以及根与系数的关系列式可得x
1=y
2,x
2=y
1,然后利用“边角边”证明△AOM和△BON全等,根据全等三角形对应边相等可得OA=OB;
(2)①过O作OC⊥AB于点C,根据等腰三角形三线合一的性质可得∠AOC=∠BOC=22.5°,再根据全等三角形对应角相等可得∠AOM=∠BON=22.5°,然后利用“角角边”证明△AOM、△AOC、△BOC、△BON全等,根据全等三角形的面积相等可得△AOB的面积等于△AOM与△BON的面积的和,再根据反比例函数系数的何意义解答;
②设直线AB与y轴的交点为D,利用直线解析式求出点D的坐标,从而得到OD的长度,再根据等腰直角三角形的性质求出OC的长度,也就是OM、ON的长度,然后根据点P在第一象限写出坐标即可.
点评:本题综合考查了反比例函数的问题,主要利用了联立两函数解析式求交点坐标的方法,一元二次方程根与系数的关系,反比例函数系数的几何意义,全等三角形的判定与性质,等腰三角形三线合一的性质,等腰直角三角形的性质,综合性较强,难度较大,考虑利用根与系数的关系的关系求解是本题的关键,也是突破口.

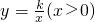 交于A、B两点,连接OA、OB,AM⊥y轴
交于A、B两点,连接OA、OB,AM⊥y轴 于M.BN⊥x轴于N;
于M.BN⊥x轴于N;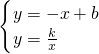 得,x2-bx+k=0,
得,x2-bx+k=0, 上,
上,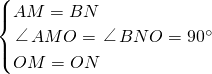 ,
,
 (90°-45°)=22.5°,
(90°-45°)=22.5°, x1•y1=
x1•y1= k,S△BON=
k,S△BON= x2•y2=
x2•y2= k,
k, k+
k+ k=k;
k=k; ×2=
×2= ,
, ,
, ,
, ).
).


 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=