
如图P是∠BAC内的一点,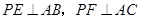 ,垂足分别为点
,垂足分别为点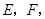
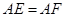 .
.
求证:(1)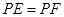 ;
;
(2)点P在∠BAC的角平分线上.
(1)连结AP,由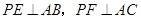 可得∠AEP=∠AFP=
可得∠AEP=∠AFP=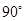 ,再结合AE=AF,公共边AP=AP,即可证得Rt△AEP≌Rt△AFP,从而得到结论;
,再结合AE=AF,公共边AP=AP,即可证得Rt△AEP≌Rt△AFP,从而得到结论;
(2)由(1)中Rt△AEP≌Rt△AFP可得∠EAP=∠FAP,从而得到结论.
【解析】
试题分析:(1)连结AP,
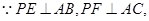
∴∠AEP=∠AFP=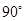
又AE=AF,AP=AP,
∴Rt△AEP≌Rt△AFP,
∴PE=PF;
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.
考点:全等三角形的判定和性质,角平分线的判定
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中极为重要的知识点,一般难度不大,需熟练掌握.


科目:初中数学 来源: 题型:
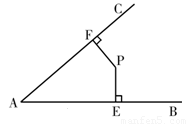
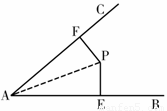
 22、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
22、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.查看答案和解析>>
科目:初中数学 来源: 题型:
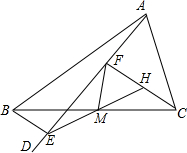 如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )
如图,△ABC中,AD是∠BAC内的一条射线,BE⊥AD,且△CHM可由△BEM旋转而得,延长CH交AD于F,则下列结论错误的是( )| A、BM=CM | ||
B、FM=
| ||
| C、CF⊥AD | ||
| D、FM⊥BC |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏扬州邗江七年级下学期第一次期末模拟考试数学卷(带解析) 题型:解答题
已知:如图,点D是∠BAC内的一点,连接BD、DC,∠A=30°,∠B+∠C=70°求∠BDC的度数.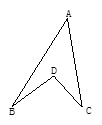
查看答案和解析>>
科目:初中数学 来源:2013届四川省盐边县红格中学九年级下学期摸底考试数学试卷(带解析) 题型:解答题
如图P是∠BAC内的一点,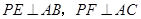 ,垂足分别为点
,垂足分别为点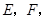
 .
.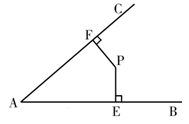
求证:(1)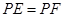 ;
;
(2)点P在∠BAC的角平分线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com