
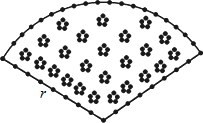
 如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3) 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
 已知:如图,在平面直角坐标系xOy中,抛物线y1=ax2+bx过点A(6,0)和点B(3,
已知:如图,在平面直角坐标系xOy中,抛物线y1=ax2+bx过点A(6,0)和点B(3,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知A、B两点被一个池塘隔开,无法直接测量,但两点可以到达,现给出一种方案:找两点C、D,使AD∥BC,且AD=BC,量出CD的长即得AB的长.其理由是
如图,已知A、B两点被一个池塘隔开,无法直接测量,但两点可以到达,现给出一种方案:找两点C、D,使AD∥BC,且AD=BC,量出CD的长即得AB的长.其理由是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,二次函数y1=ax2+bx+c(a≠0)的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.
如图,二次函数y1=ax2+bx+c(a≠0)的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据
如图,小明在商贸大厦离地面25m高的A处看地面C处汽车,测得俯角为45°,小明上升5m后到B处看到该汽车行驶到D处,测得俯角为60°,若汽车在与该楼的垂直线上行驶,求汽车行驶的距离CD的长.(结果精确到0.1米,参考数据| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为13米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).
某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为13米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com