Question

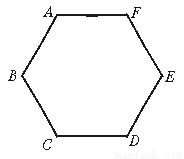
下图是正六边形ABCDEF，它的边长为2，请你建立适当的直角坐标系，把各顶点的坐标写出来.

 

Answer 1

【答案】

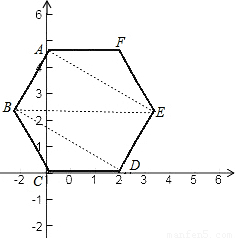
如图所示以C点为原点建直角坐标系，

则A（0，2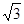），B（-1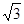，），C（0，0），D（2，0），E（3，2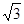），F（2，2）．

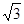【解析】

试题分析：根据题意建立直角坐标系，再利用正六边形的内角和公式，求得内角和，利用正六边形各个角都相等的性质，求得每一个内角角度；抓住三角形的性质，求得各顶点坐标．

如图所示以C点为原点建直角坐标系，

则A（0，2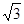），B（-1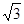，），C（0，0），D（2，0），E（3，2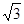），F（2，2）．

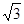考点：本题考查的是坐标与图形性质

点评：再解答过程中，综合运用了正六边形的性质、等腰三角形的性质、平行线的性质．所以必须牢记各种图形的性质，才会避免在做题过程中造成知识的混淆．