
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
先阅读下面两个简单的推理,然后解决问题:
①对于任意实数x,
∵x2≥0 ,
∴x2+1>0;
②对于任意实数x,
∵(x-![]() )2≥0,
)2≥0,
∴(x-![]() )2+
)2+![]() >0
>0
问题:
1.求证:对于任何实数,均有2x2+4x+3>0
2.先在下面的括号内填上适当的选项,再证明你的结论.
设M=3x2-5x-1,N=2x2-4x-7,则( )
A. M>N B.M<N C.M≥N D.M≤N
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级上学期期中数学卷 题型:解答题
先阅读下面两个简单的推理,然后解决问题:
①对于任意实数x,
∵x2≥0 ,
∴x2+1>0;
②对于任意实数x,
∵(x-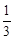 )2≥0,
)2≥0,
∴(x-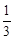 )2+
)2+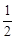 >0
>0
问题:
1.求证:对于任何实数,均有2x2+4x+3>0
2.先在下面的括号内填上适当的选项,再证明你的结论.
设M=3x2-5x-1,N=2x2-4x-7,则( )
A. M>N B.M<N C.M≥N D.M≤N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com