练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    直线L上有一点P到圆心O的距离为3cm，⊙O的半径也为3cm，则直线L与⊙O的位置关系是


    1. A.
      相切
    2. B.
      相交
    3. C.
      相切或相交
    4. D.
      无法确定
    C
    分析：没有明确OP的长度就是圆心到直线的距离，所以直线与圆的位置关系要分情况讨论．
    解答：由于OP=3cm，且O为圆心；
    ①当OP⊥直线L时，圆心到直线L的距离等于半径，即直线L与⊙O相切；
    ②当OP不与直线L垂直时，根据“垂线段最短”知：圆心O到直线L的距离要小于⊙O的半径，即直线L与⊙O相交；
    因此存在两种位置关系：相切或相交，故选C．
    点评：考查直线与圆位置关系的判定．要掌握半径和圆心到直线的距离之间的数量关系，本题中P到圆心的距离没有明确是圆心到直线的距离，所以运用分类讨论是正确解题的关键所在．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    12、下列说法不正确的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6、下列说法中，正确的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

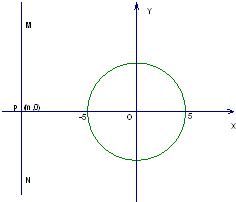    8、如图，在平面直角坐标系中，以O为圆心，5个单位为半径画圆．直线MN经过x轴上一动点P（m，0）且垂直于x轴，当P点在x轴上移动时，直线MN也随着平行移动．按下面条件求m的值或范围．
    （1）如果⊙O上任何一点到直线MN的距离都不等于3；
    （2）如果⊙O上有且只有一点到直线MN的距离等于3；
    （3）如果⊙O上有且只有二点到直线MN的距离等于3；
    （4）随着m的变化，⊙O上到直线MN距离等于3的点的个数还有哪些变化？请说明所有各种情形及对应的m值或范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    （2013•西城区一模）先阅读材料，再解答问题：
    小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D＞∠E．
    请你参考小明得出的结论，解答下列问题：

    （1）如图1，在平面直角坐标系xOy中，点A的坐标为（0，7），点B的坐标为（0，3），点C的坐标为（3，0）．
    ①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；
    ②若在x轴的正半轴上有一点D，且∠ACB=∠ADB，则点D的坐标为
    （7，0）
    （7，0）
    ；
    （2）如图2，在平面直角坐标系xOy中，点A的坐标为（0，m），点B的坐标为（0，n），其中m＞n＞0．点P为x轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：三点一测丛书　九年级数学　上　（江苏版课标本） 江苏版课标本 题型：022

    圆中的最值问题

    如图，点A是半圆上一个三等分点，点B是的中点，点P是半径ON上的动点．若⊙O的半径为1，则AP＋BP的最小值为________．

    分析：解决此问题的数学模型是：在直线l的同侧有两定点A、B，试在直线l上确定一点P，使AP＋BP最小．这就要用到轴对称和“两点之间，线段最短”的知识点．

    作点B关于MN的对称点，连结，交MN于点P，则此时AP＋BP的值最小．

    请根据以上分析求出AP＋BP的最小值．

    查看答案和解析>>

    同步练习册答案